Siraküza kuşatması ve uygulamalı matematik

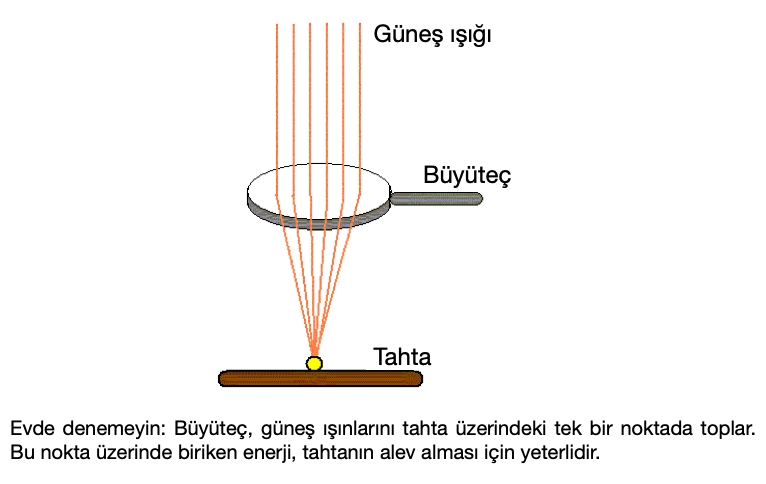
Çoğumuz çocukluğumuzda büyüteç ile tahta veya kâğıt yakmıştır. Güneşli bir günde dışarı çıkarsınız, büyüteci tahta ve güneş arasına koyarsınız, büyüteçten yansıyan güneş ışınları tahta üzerine tek bir noktada yoğunlaşana kadar büyüteci aşağı yukarı hareket ettirirsiniz. Büyüteç üzerine düşen güneş ışınları, tek bir noktada toplandıkları zaman tahtanın tutuşması için gerekli enerji birikmiş olur. Bu haftaki yazımızda, bu deneyin teorik arka planını ve Arşimet’in bu prensibi kullanarak Roma gemilerini nasıl yaktığını anlatacağız.

[BAA - Matematik]

Paraboller

Paraboller, lise geometri derslerinin en temel konularından bir tanesidir. Bir \(l\) doğrusu ve bu doğru üzerinde olmayan bir \(p\) noktası verildiğinde, düzlemde \(l\) doğrusu ve \(p\) noktasına eşit uzaklıkta bulunan noktaların kümesine parabol denir. \(l\) doğrusu, parabolün doğrultmanı, \(p\) noktası da parabolün odak noktası olarak adlandırılır.

Parabol; çember, elips ve hiperbol ile birlikte Antik Yunan geometricilerinin “konik kesitler” olarak adlandırdığı eğrilerden bir tanesidir. Konik kesitler, uzun bir süre dönemin geometrisinin en temel çalışma nesnelerinden biri olmuş; Arşimet ve Öklid’in çalışmalarını tamamlayarak günümüzde bu eğrilerin modern matematikte kullanılan tanımlarını veren ve onları sınıflandıran Pergeli Apollonius’un (M.Ö. 240 – M.Ö. 190) çalışmalarıyla en üst düzeye ulaşmıştır. Antik Yunan matematikçilerinin bu eğriler üzerine çalışmasının çok doğal bir sebebi vardır: Bu şekillerin hepsi, düzlemde ikinci dereceden bir denklemin çözüm kümesidir. Yani, elips, hiperbol ve paraboller, verilen katsayılar için

\( Ax^2 + Bxy + Cy^2+Dx+Ey+F = 0\)

denklemini sağlayan \( (x,y) \) noktalarının kümesi olarak yazılabilir. Denklem, indirgenemez ise -yani çözüm kümesi iki doğrunun birleşimi olarak yazılamıyor ise- bu denklemin çözüm kümesinin elips mi, hiperbol mü yoksa parabol mü olduğunu anlamanın kolay bir yolu vardır. Diskriminant olarak da adlandırılan ve eğrilerin sınıflandırılmasına yarayan \(\Delta=B^2-4AC\) değeri eğer 0’a eşitse, çözüm kümesi bir paraboldür. Eğer \(\Delta<0\) ise elips, \(\Delta>0\) ise hiperbol elde ederiz. Örneğin, \(y-x^2=0\) denklemi için \(A=-1, B=0\) ve \(C=0\) olduğu için \(\Delta=0\) olur. Haliyle \(y-x^2=0\) denklemi bir parabol tanımlar.

Parabollerin, yazımız için önemli olan bir özelliği bulunmaktadır. Parabolün iç yüzeyinin ışığı yansıttığını varsayalım. Bu durumda, doğrultmana dik olarak gelen ışınlar, parabolden yansırken odak noktasından geçerler. Bu özelliğin kanıtını bu yazıda vermeyeceğiz fakat teoremi kanıtlamayı denemek isteyen okurlar için bir kolaylık sağlayabiliriz. Düzlemde bütün paraboller birbirlerine “benzer” oldukları için, teoremi \(y-x^2=0\) parabolü için kanıtlamak yeterlidir.

Siraküza Kuşatması

M.Ö. 213 yılında Roma Cumhuriyeti, Antik Yunan şehir-devleti Siraküza’ya savaş ilan etti ve şehri gemileriyle kuşattı. Siraküza’nın şansına, şehri savunanlar arasında tarihin en büyük matematikçilerinden biri olan Arşimet (M.Ö. 287 - M.Ö. 212) de vardı. Romalılar, sambuca denilen ve gemilerden şehir duvarlarına köprü yaslamak için kullanılan icatlarını ilk defa bu savaşta kullanırken, Arşimet de bu yeni tekniklere kendi icatlarıyla karşılık verdi. Arşimet’in icatlarından bir tanesi “Arşimet pençesi” denilen ve şehrin duvarından dışarıya uzatılabilen uzun, tahta pençelerdi. Siraküzalı askerler, şehir duvarlarının arkasından bu pençeler yardımıyla bir gemiyi tuttuktan sonra yukarı kaldırıp hızla bırakarak onları batırabiliyorlardı (Arşimet’in ünlü sözünü hatırlayın: “Bana bir dayanak noktası gösterin, dünyayı yerinden oynatayım.”).

Arşimet’in yazımızın ilk bölümüyle ilgili olan icadı ise parabolik aynalardı. Arşimet, cilalanmış kalkanları bir araya getirip, bir parabol oluşturacak şekilde bir araya getirdi. Bu aynalar, şekilleri sayesinde tek bir odak noktasına sahiptiler. Bir önceki bölümde bahsettiğimiz teoreme göre, bu aynalardan yansıyan Güneş ışığı tek bir noktada toplanıyordu. Arşimet, bu aynaları şehir duvarlarına ve şehrin etrafındaki tepelere yerleştirerek şehir duvarlarına yaklaşan Roma gemilerini yakabiliyordu.

Arşimet’in bu dahiyane icatları bile Siraküza’yı uzun süre koruyamadı. Bir yıldan uzun süren kuşatma, Siraküzalıların kutlama yaptıkları bir esnada bir grup Roma askerinin şehre sızıp kapılarını Roma ordusuna açmasıyla sona erdi. Tarihçi ve filozof Plutark’ın anlatımına göre, kuşatma sona erdiği sırada Arşimet bir matematik problemi ile uğraşıyordu. Roma ordularının komutanı Marcus Claudius Marcellus, kuşatmanın bu kadar uzun sürmesine neden olan büyük matematikçi ile tanışmak için bir askerini yolladı ve Arşimet’e kesinlikle zarar verilmemesini emretti. Arşimet, bu esnada bir matematik problemi ile uğraşıyor ve kum üzerine geometrik şekiller çiziyordu. Askeri “Çemberlerimi bozma” diyerek azarlayan Arşimet, Marcellus’u ancak uğraştığı problemi çözdükten sonra göreceğini söyleyerek çağrıyı reddetti. Bu beklenmedik cevap karşısında hiddetlenen asker, General Marcellus’un emirlerini hiçe sayarak bu büyük matematikçiyi öldürdü.

Uygulamalı Matematik

Arşimet’in icatlarını, matematiğin bir dalı olan “uygulamalı matematiğin” ilk örneklerinden biri olarak değerlendirebiliriz. Parabollerin yansıtma özelliği ile ilgili teorem, Arşimet’ten önce kanıtlanmış ve Arşimet dönemindeki pek çok geometrici tarafından bilinen bir teoremdi. Fakat, herkesin bildiği bu teoremden işimize yarayan bir alet çıkarmak da en az teoremi kanıtlamak kadar yaratıcılık ve zekâ gerektiren bir iştir. Uygulamalı matematikçiler, tıpkı Arşimet’in yaptığı gibi, insanların karşılaştıkları bir problemi alıp, önce onu bir matematik problemine dönüştürmeye çalışırlar. Sonra da ya önceden kanıtlanmış teoremleri kullanarak ya da bizzat kendileri problemi çözmelerini sağlayacak teoremleri oluşturarak bu matematik problemine bir çözüm getirirler. Tabii ki, içinde yaşadığımız dünyanın bir “matematiksel model”ini oluşturmak mümkün değildir. Gerçeklik ile onun matematiksel modeli arasında zorunlu olarak her zaman bir açı olacaktır. Neyse ki, modellerimizin işe yaraması için bu açının çok küçük olması gerekmez. Eğer gerçekliğin bütün karmaşıklığı ve ayrıntılarını modelimize yansıtmaya çalışırsak model çok karmaşık olur ve teoremlerimiz bu modelden gerekli bilgiyi çıkarmak için yeterli olmayabilir. Bu nedenle, modellerimizin oldukça basit olmasını ve gerçekliğin sadece işimize yarayacak olan kısmını yansıtmasını isteriz. Şu soru akla gelebilir: Matematiksel model gerçeklikle aynı olmadığı halde, nasıl oluyor da modeli kullanarak oluşturduğumuz aletler işe yarayabiliyor? Bunun için, model ile gerçeklik arasındaki farkı kontrol edebiliyor olmamız gerekir. Arşimet örneğine dönersek, Güneş ışınları, tek bir nesneden yani Güneşten geldiği için aslında birbirlerine paralel değildir. Bu nedenle parabollerin yansıtma prensibine göre hareket etmezler, yani parabolik aynalardan yansıyan ışınlar tek bir odak noktasından geçmezler. Fakat, Dünya Güneş’ten çok uzak mesafede olduğu için, Güneş ışınları arasındaki açı çok küçüktür ve aynadan yansıyan ışınlar odak noktasından geçmese bile odak noktasına çok yakın bir noktadan geçerler. İcadımızın çalışacağından emin olmak için, Güneş ışınlarının odak noktasından ne kadar uzaktan geçebileceğini de hesaplamamız gerekir.

Kapanış notu: Muhtemelen gerçek olaylara dayanan güzel bir hikâyeyi, gerçeklere sıkı sıkıya bağlı kalarak berbat etmek gibi bir vulgarlıktan uzak durmak için yazımızda bahsetmesek de Arşimet’in gerçekten Siraküza kuşatması esnasında parabolik aynalar yardımıyla Roma gemilerini yakıp yakmadığı bir tartışma konusudur. İnternette kısa bir araştırmanın göstereceği üzere, Arşimet’in aynalarını o dönem kullanılan tekniklerle oluşturan ve bu nedenle hikâyenin gerçek olabileceğini iddia eden pek çok deney olduğu gibi, Arşimet’in böyle bir aynayı yapamayacağı, yapsa bile gerek gemilerin hareket etmesi, gerekse gemilerin alev almasının çok uzun süreceği gibi gerekçelerle bu hikayeyi çürüten pek çok makale vardır. Meraklı okuyuculara MythBusters dizisinin 2. sezonunun 8. bölümü ve 4. Sezonun 3. bölümünü izlemelerini öneririz.

Kaynaklar

1. Renyi, Alfred. Dialogues on Mathematics. 1996, Dost Kitabevi
2. Wikipedia : https://en.wikipedia.org/wiki/Siege_of_Syracuse
3. Dallow, A. Ve Lentle T. (2003-2016), MythBusters, Discovery Channel