Polinomların Radikallerle Çözümleri ve Galois'nın Mirası

Matematik tarihinde Évariste Galois'nın hayatı kadar trajik olan çok az örnek vardır sanırım. Zamanının politik ortamında hiç çekinmeden cumhuriyet saflarında yerini alan Galois, sadece bu devrimci tutumuyla değil aynı zamanda matematik alanında çığır açan buluşlar yapmasıyla da tarihi etkilemiştir.

[BAA - Matematik / Erman Işık]

Évariste Galois 25 Ekim 1811 tarihinde Nicholas-Gabriel Galois ve Adélaïde-Marie çiftinin çocukları olarak Paris'e yakın bir konumda olan Bourg-la-Reine kasabasında dünyaya gelir. Babası kasabadaki liberal parti üyesi bir cumhuriyetçidir ve 1814 yılında kasabanın belediye başkanı dahi olur. Ancak 28 Temmuz 1829’da kasabanın rahibi ile aralarında geçen şiddetli bir politik tartışmadan sonra Galois’nın babası intihar eder. Bir hukukçunun kızı olan annesi, Latinceye son derece hakimdir ve klasik edebiyat ile yakından ilgilenmektedir ve zamanına göre bir kadın için iyi bir eğitim almıştır. Bunun sonucu olarak oğullarının ilk on iki yıllık eğitimini kendisi verir.

Évariste, 14 yaşında matematiğe ciddi bir ilgi göstermeye başlar. Henüz 15 yaşındayken, Joseph-Louis Lagrange (1736-1813)'ın Denklemlerin Cebirsel Çözümü Üzerine Düşünceler (Réflexions sur la résolution algébrique des équations) gibi onu denklemler kuramı alanında çalışmaya teşvik edecek kitapları okumaktaydı. Buna karşın matematik dışındaki dersler ilgisini çekmiyordu. Bu yüzden diğer derslere çalışmaması gibi bir dizi nedenden dolayısıyla okulda başarılı olamıyordu. Galois 1828 yılında hiçbir hazırlık yapmaksızın o zamanlarda Fransa’daki en ünlü matematik enstitüsü ve okulu olan École Polytechnique’ nin sınavlarına girmeyi dener ve sözlü sınavlardaki açıklama yetersizliklerinden ötürü başarısız sayılır. Aynı yıl École Normale adlı matematik okuluna kabul alır.

1829'da babasının intiharından birkaç gün sonra Évariste Polytechnique’e girmek için şansını tekrar dener ancak yine başarısız olur. Évariste konuları çok fazla açıklamadan anlatıyor bu durum da sınavı yapan kişinin kafasının karışmasına neden oluyordu. Sonuç olarak çok fazla sinirlenen Galois kendine hakim olamıyor ve komisyon üyeleriyle tartışıyordu. Hatta sınav komisyonundan birisine silgi fırlattığı da anlatılan anekdotlardan biridir.  

1830 yılı Fransa'da devrim rüzgarlarının yeniden estiği yıldır. XVIII. Louis'nin 1824'te ölümü üzerine iktidara geçen X. Charles, ağabeyinin aristokrasi ve sermaye sınıfı arasındaki denge politikasını terk etmekte, öte yandan aristokrasiyi ve kiliseyi güçlendiren bir politika izlemekteydi. Bu siyasi adımlar halkta tepkilere neden oluyordu. X. Charles'ın 1830'da meclisi feshetmesi bardağı taşıran son damla olur; Paris'te yeniden barikatlar kurulur...

Genç matematikçi derhal devrimci bir grup olan Halkın Dostları (Société des Amis du peuple)'nın bir üyesi olur ve Ulusal Topçu Alayı’na katılır. Bu zamanlarda matematik çalışmasını da bırakmayan Galois daha önce reddedilen iki yazısından sonra üçüncü ve son defa Denklemlerin Köklerle Çözülebilirliği Koşulları Üzerine (Mémoire sur les conditions de résolubilité des équations par radicaux) başlıklı yazısını Fransız Bilimler Akademisi’ne sunar.

Galois Akademi'den cevap beklerken mücadeleye de devam etmekteydi. 9 Mayıs' ta Cumhuriyetçilerin mitingine ve ardından yemeğine katılır. Bu yemekte kadehini üzerine bir bıçak koyarak yeni Kral Louis Phillippe'e kadeh kaldırmayı teklif eder. Ertesi sabah polis Galois'nın odasını basıp onu tutuklar. Galois bir ay tutuklu kalır ve sonrasında serbest bırakılır.

Galois bu defa da Louis Phillippe'in yasaklamış olduğu Topçu Alayı'nın üniformasını giydiği için tutuklanır ve altı ay hapis cezasına çarptırılır. Hapisteyken Galois Akademi sekreterinden çalışmasının yanıtı alacaktır. Fakat yanıt yine Galois için olumsuzdur. Sekreter, Galois'dan çalışmalarını açıklamasını istiyor ve bu durum gerçekleşene kadar yazının yayınlanmasının beklemesi gerektiğini söylüyordu.

Hapis ve bunun üzerine akademi dünyası tarafından dışlanmak Galois'nın sağlığını olumsuz yönde etkiler... Bu nedenle Mart 1832'de bir şifa yurduna gönderilir. Burada başka bir cumhuriyetçi olan Eve Sorel ile tanışır ve ondan hoşlanır...

Paris'i kasıp kavuran korkunç kolera salgını geçtikten ve Galois sağlığına kavuştuktan sonra serbest bırakılır. Birkaç gün sonra, bir gece, Eve Sorel ile ilişkisi olduğunu iddia eden bir kişi caddede Galois'nın yanına gelir ve aralarında tartışma çıkar... Bunun sonucu bu yabancı ertesi sabah bir düello için Galois'ya meydan okur. Bu noktada bazı tarihçilerin meydan okuyan kişinin usta bir silahşör olduğunu ve Galois'yı ortadan kaldırmak için polis tarafından gönderildiğini düşündüğünü de belirtmemiz gerekiyor...

Galois hemen evine gider ve çalışmalarını açıklamak için masasının başına geçer. Sabaha kadar mum ışığında o güne kadar yaptığı bütün çalışmalarını gözden geçirir ve sonuçlarını, birisi arkadaşı Auguste Chevalier (1873-1956) diğeri kopyası ise bir yoldaşına gönderilmek üzere, iki mektup haline getirir.

Ertesi sabah hava kasvetli ve kurşunidir... İki düellocu saat 5.00 sularında buluşurlar ve karanlık yürüyüşlerine başlarlar. Birkaç dakika sonra, usta rakibine karşı hiçbir şansı olmayan genç Galois karnından vurularak yere düşer... Ertesi gün 31 Mayıs 1832 tarihinde genç dahi hayata gözlerini yumdu.  

Galois'nın eserlerinin talihi kendi talihinden daha iyidir, çünkü can dostu Chevalier mektubu gerekli yerlere iletmiştir ve bir sonraki yıl Revue Ansiklopedisi (Revue Encyclopedique)'de Galois'nın son yazısının basılmış olduğunu görmüştür. Nihayet 1870 yılında meşhur matematikçi Camille Jordan (1838-1922) Galois'nın teorilerinin önemini kavrar ve bu teorileri kendi kitabına ekler. Bunun neticesinde Jordan'ın eseri meşhur, Galois'nın fikirleri de ölümsüz olur...

13 Haziran 1909'da Bourg-la-Reine'de, kasabanın ihmal edilmiş bireyinin onuruna parlak bir tören yapılır. Bu törende belediye başkanı, ünlü matematikçiler, önemli bürokratlar ve Fransız Bilimler Akademisi'nin sekreteri hazır bulunuyordu ve Galois'nın devam etmiş olduğu üniversite hazırlık okulu müdürünün konuşması şu cümlelerle biter: ''Bizler, girdiğine pişman olduğu, yanlış anlaşıldığı, kovulduğu ve en canlı övünç kaynağı olduğu bu okul adına Galois'nın dehasından özür dilemek için burada bulunmaktayız.''

Radikallerle Çözmek

Matematikte, çeşitli türde denklemlerin çözümleri çok önemli bir yer tutar. Çünkü doğada gözlemlediğimiz bir olguyu ya da matematiğin kendi içindeki bir araştırmayı hemen her zaman denklemlere ve onların çözümlerini araştırmaya indirgeriz. İşte 21 yaşında yaşama veda eden Évariste Galois bize polinom denklemleri adını verdiğimiz denklemlerin çözümlerini araştırmak için devrim niteliğinde bir miras bıraktı.

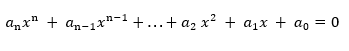
tipindeki denklemlere polinom diyoruz ve bu denklemleri radikallerle çözmek derken de denklemin çözümünü veren sayıyı denklemin katsayıları dediğimiz

sayılarını toplama, çıkarma, çarpma, bölme veya kök alma işlemini (karekök, küpkök vb.) uygulayarak yazabilmeyi anlıyoruz. Bir örnekle açıklayayım, mesela

ikinci dereceden bir polinom denklemidir ve

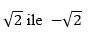
bu denklemin çözümleridir. İkinci dereceden polinom denklemleri dediğimiz  

formundaki denklemlerin radikaller ile çözümünü 9. yüzyılda yaşamış olan Fars matematikçi Ebû Ca'fer Muhammed bin Mûsâ el-Hârezmî' nin yazdığı Cebir ve Karşılaştırma Hesabı Üzerine Özet Kitap (الكتاب المختصر في حساب الجبر والمقابلة‎ al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala)  aracılığıyla biliyoruz. Modern kavramlarla artık bu tür polinomların çözümlerinin  

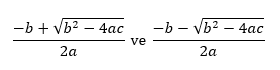
olduğunu liselerde öğretiyoruz (ya da ezberletiyoruz demek daha doğru olur sanırım).

Üçüncü ve dördüncü dereceden denklemlerin çözümleri ise 16. yüzyıla kadar beklemek zorunda kaldı. İtalyan matematikçi Gerolamo Cardano (1501-1576)’nun 1545' te yayımladığı Büyük Sanat (Ars Magna) adlı eserinde bazı çağdaşlarının yaptıklarından yararlanarak üçüncü dereceden denklemlerin çözümünü verdi. Bu kitapta Cardano'nun öğrencisi Lodovico Ferrari'nin (1522-1565) bulduğu dördüncü dereceden denklemlerin çözümü de var. Bütün bu gelişmeler zamanın bilimsel birikimine önemli katkılar olmasına rağmen hala daha büyük dereceli sonsuz tane denklemin çözümünü, katsayıları aracılığıyla yazıp yazamayacağımıza bir cevap verebilmiş değiliz! Bu cevap için Galois'nın dehasına ve inatçılığına ihtiyacımız vardı.

Galois'nın soruyu nasıl ele aldığına ve çözüme nasıl ulaştığına bakmadan önce sayılara ve simetrilere hızlıca bir göz atmamız faydalı olacaktır sanırım.

Sayılar ve Cisimler

Günlük hayatta 1,2,3,… gibi sayıları sıkça kullanırız. Bu sayılara doğal sayılar denir. Ayrıca 0 sayısı ve negatif sayılar da var -1,-2,…. Bu sayıların hepsine birden ''tam sayılar'' adı verilir. Fakat daha genel sayılar da vardır ve polinom denklemlerinin çözümlerini araştırmak için onları da hesaba katmalıyız. 2,25 TL gibi bir ifade ile karşılaştığımızda aslında rasyonel sayılar dediğimiz sayı gruplarından bahsetmiş oluyoruz. 2,25 TL aslında 2 ile 25/100 kesrinin toplamıdır.

Keyfi bir m tam sayısı ve sıfırdan farklı bir n tam sayısı için, rasyonel sayılar m/n şeklinde gösterilirler ve bütün rasyonel sayılarla toplama, çıkarma, sıfır dışındaki rasyonel sayılar ile de çarpma ve bölme işlemleri yapabiliriz. Bu işlemlerin hepsine birden aritmetik işlemler diyelim; yani rasyonel sayılar üzerinde aritmetik yapabiliriz. Üzerinde aritmetik yapabildiğimiz matematiksel yapılara cisim diyoruz.

Cisimler üzerinde aritmetik yapılabildiği için matematikçiler için çok verimli yapılardır. Dahası, onları polinomlar aracığıyla elde edebildiğimiz için bizim için ayrıca önemli bir konuma sahip. Şimdi de bir polinomdan cisim elde etmekten neyi kastettiğimizi açıklayalım:

Elimizde x²-3=0 polinomu olduğunu kabul edelim. Bu polinomun bir kökünün √3 olduğunu biliyoruz. Ayrıca bu polinom bir başka kök daha sahip, -√3 . Şimdi √3'ü rasyonel sayılara eklemek için sistemli bir yol inşa etmeye çalışalım. Rasyonel sayıları bir bardak çay gibi düşünün. Çaya şeker ilave ederek tatlandırabilirsiniz. Şekeri ekledikten sonra yine elimizde bir bardak çay vardır ama artık istediğimiz tattadır. İşte şeker ilave etme işlemini rasyonel sayılara √3 eklemek gibi düşünürsek işlemin sonunda yine aritmetik yapabildiğimiz bir yapı elde etmek de çayın tatlanması olacak.

İlk önce bu yeni yapıdaki bir elemanı nasıl ifade edeceğimizi belirtmemiz lazım ki aritmetik yapabilelim. Bu yeni yapı rasyonel sayıları içereceği için içerisinde, keyfi bir m tam sayısı ve sıfırdan farklı bir n tam sayısı için m/n şeklinde ifade edilen elemanlar bulunmak zorunda. Fakat biz çarpma yapmak istediğimizi de belirtmiştik, dolayısıyla rasyonel sayıları √3 ile çarptığımız sayıları da bu kümede görmemiz gerekir. Yani, (m/n)√3 formundaki sayılar da bu küme içerisinde. Bunları birbirleriyle toplamak istediğimiz için de, keyfi m,k tam sayıları ve sıfırdan farklı n,l tam sayıları için m/n + (k/l)√3 toplamlarını da dahil etmeliyiz. İşte bu formdaki sayıları içeren kümenin tamamı bizim rasyonel sayılara √3 ekleyerek elde ettiğimiz sayı cismini oluşturur. Burada çarpma veya toplama yaparken kesirli sayılardaki kuralların yanı sıra sadece √3'ü kendisiyle çarptığımızda 3 tamsayısını elde edeceğimizi dikkate almamız yeterlidir. Örneğin,

elde ederiz ve sonuç yine bizim sayı cismimizin içindedir.

Yukarıda x²-3=0 polinomu için yaptığımız işlemin aynısını herhangi bir  polinoma uygulayabiliriz*. Yani bu polinomun varsayımsal olarak bir çözümü** α olsun. Bu sayıyı rasyonel sayılara yukarıdaki adımlara benzer adımlarla katabiliriz ve sonuçta elimizde rasyonel sayıları içeren ve aritmetik yapabildiğimiz yeni bir yapı elde ederiz. Hem de polinomumuzun bir çözümü de içerisinde bulunmakta!

Simetriler

Artık bir polinomun köklerinin ifadesini ararken elimizde yeni bir yapı var, cisimler. Polinomun kendisiyle ilgilenmek yerine onunla yakından ilişkili olan sayı cismini incelememiz bize daha fazla avantaj sağlayacak. Ancak genel kanının aksine matematiksel yapılar durağan değil tıpkı fiziksel dünyadakiler gibi hareket halindedir. Mesela bir trenin hızıyla ya da konumuyla ilgili çalışma yapılırken treni hareket halindeyken modelleriz. Matematiksel yapılar da tek başına incelenmenin yanı sıra onları hareket ettiren etkilerle birlikte incelenir. Bu etkiler fonksiyon olarak tanımlanır ama daha özel fonksiyonlara özel isimler de verilir. Biz bizim cismimizin hareketine sebep olan etkilere simetri diyeceğiz.  

Simetri nedir? Kare bir masa düşünelim ve bu masayı saat yönünde 90 derece döndürelim. Yine kare bir masa elde ederiz. İşte simetri bu döndürme hareketidir. Yani simetri derken o cismin simetrik bir şekle olmasını değil, ona uyguladığımız bir etki sonucunda yine aynı cismi elde ettiğimiz hareketi kastediyoruz. Mesela masamız kare yerine dikdörtgen olsaydı 90 derecelik döndürme bir simetri olmayacaktı, çünkü kısa ve uzun kenarlar tam aynı konumda bulunmayacaktı ama 180 derece döndürme dikdörtgen masanın bir simetrisidir.

Yine kare masa örneğinden devam edelim ve simetriler hakkında biraz daha akıl yürütelim. Masamızın başka simetrileri de vardır; 180, 270, 360 derece döndürmeler gibi. Peki iki simetriyi art arda uygulasak ne olur? 90 ve 180 dereceyle belirttiğimiz simetrileri art arda uygulasaydık aslında 270 derecelik simetriyi elde edecektik. Bu genel olarak da doğru. Yani iki simetriyi art arda uygulamak yine bir simetridir.

360 derecelik simetrimiz masamızı ilk konumunda bırakmakla aynı şey. Bu nedenle sabit bırakma da bir simetri. Son olarak şu gözlemi de yapalım. Mesela 90 derecelik simetriyi uyguladıktan sonra 270 derecelik simetriyi uygularsak sabit bırakma simetrisini elde ederiz. Yani şunu söyleyebiliriz; bir simetri için öyle başka bir simetri vardır ki bu simetrileri art arda uyguladığımızda sabit bırakma simetrisini elde ederiz. İşte bu üç özelliği sağlayan yapılara grup*** diyoruz. Yani bir cismin bütün simetrilerinden oluşan yapı bir grup yapısına sahiptir.

İşte Galois rasyonel sayılara polinomun köklerini katarak elde ettiğimiz cisimlerin simetrileri olduğunu keşfetti. Bu simetriler grup yapısına sahipti ve bu grupları anlamak polinomlar hakkında bilgi edinmenin çok verimli bir yoluydu.

Mesela eğer polinomuzun köklerini eklediğimiz cismin simetrileri ''çözülebilir grup'' dediğimiz gruplarsa, yani çözülebilir gruplar için sağlanan ekstra koşulu sağlıyorsa, o polinomun kökleri yukarıda belirttiğimiz anlamda radikaller şeklinde yazılabilir. Yani kökleri katsayıları toplama, çıkarma, çarpma, bölme veya kök alma yoluyla bulabiliriz.  

Derecesi 2,3 ya da 4 olan bütün polinomların simetri grupları çözülebilir gruplardır. Fakat derecesi 5 olan bütün polinomlar için simetri grupları çözülebilir grup değildir. Yani derecesi 5 olan polinomları radikallerle çözemeyiz!

İşte Galois hem sonsuz tane polinom denklemini ele almanın sistematik bir yolunu bulduğu hem de bize bugün bile kullandığımız yeni ve çığır açıcı yaklaşımları geliştirdiği için önemli ve saygıdeğerdir.

Notlar

* Aslında burada herhangi bir polinom yerine diğer polinomları üretenpolinomları alıyoruz. Üretmekten kastımız, herhangi bir polinomu bu üreten polinom cinsinden yazmak ... -3, -2, -1, 0, 1, ,2, 3, ... gibi sayılara tam sayılar adı verildiğini söylemiştik. Tam sayıların en güzel özelliklerinden bir tanesi de herhangi bir tam sayının bazı sayıların çarpımı şeklinde yazılabiliyor olmasıdır ki bu sayılara asal (kendisinden ve 1’den başka böleni olmayan) sayılar diyoruz. Örneğin, 49=7.7 ya da 195=3.5.13 gibi ve burada 3,5,7 ve 13 asal sayılardır. İşte polinomlar da bazı polinomların çarpımları şeklinde yazılabiliyor. Bu nedenle sadece bu asal (sayılardaki tanımı genelleyebiliriz) polinomları incelememiz yeterli.  

** Varsayımsal çözüm fazla zorlama gibi gelebilir ama bir polinomun bütün çözümlerini içeren ve rasyonel sayıları da içeren cisimlerin var olduğu kanıtlanmıştır. Mesela bizim durumumuzda bu cisim karmaşık sayılardan oluşan cismin içerisinde yaşamakta. Ayrıca çözümü bulmak derken çözümü bildiğimiz ifadelerle betimlemekten bahsediyoruz.

*** Matematik alanında bir yapıyı ifade etmek için grup kelimesini kullanan ilk kişi Galois'dır.

Kaynaklar

Frances Benson Stonaker - Famous Mathematicians, Évariste Galois, Lippincott, 1966

Halil İbrahim Karakaş - Cebir Dersleri, TÜBİTAK Yayınları, 2012

http://www.wikiwand.com/en/%C3%89variste_Galois

http://www.matematikdunyasi.org/arsiv/PDF_eskisayilar/1994_3_9_13_CEBIRSEL.pdf

https://www.matematiksel.org/cebirin-atasi-el-harezmi/