Königsberg’in Yedi Köprüsü ve Topolojinin Doğuşu

Bu yazıda matematiğin en ünlü problemlerinden biri olan Königsberg’in Yedi Köprüsü hakkında konuşacağız. Birçok yerde karşınıza çıkabilecek bu problemi ve çözümünü, Euler’in asıl makalesine sadık kalarak, tarihsel akışıyla birlikte paylaşacağız.

[BAA – Matematik/ Oğuz Şavk]

Königsberg’in kısa tarihi

Kralın dağı manasına gelen Königberg şehri 1255 yılında, bir antik Prusya yerleşim yeri olan Twangste (meşelik) bölgesinde, Tötonik (Cermen) şövalyeler tarafından Bohemia Kralı Ottokar II’yi onurlandırmak için kurulur. Bir Baltık liman şehri olan Königsberg, 1525-1701 yılları arasında Prusya Düklüğü’nün başkenti olur. 1544 yılında kurulan Albertina Üniversitesi ile birlikte Alman kültürü ve entelijansiyası ile beslenen Königsberg şehri, Simon Dach, Immanuel Kant, Kathe Kollwitz, Ernst Hoffmann ve David Hilbert gibi aydınlara ev sahipliği yapar. Aynı zamanda Pregel Nehri’nin etrafına yayılan Königsberg şehri, Orta Çağ’da bir ticaret merkezi haline gelir. 18. yüzyıla ait bir gravür bu şehri Şekil 1'deki gibi resmetmektedir.

Şekil 1’de görüldüğü gibi Pregel Nehri Kneiphof adasını çevreler ve dalları vasıtasıyla Königsberg şehri dört kara parçasına ayırır. Bu dört parçayı birleştiren, Şekil 2’de gösterildiği gibi konumlanan yedi köprünün isimleri şunlardır: Demirci’nin Köprüsü, Bağlantı Köprüsü, Yeşil Köprü, Tüccar’ın Köprüsü, Tahta Köprü, Yüksek Köprü ve Bal Köprü.

Rivayete göre şehrin insanları, güzel şehirlerinin yedi yerine konuşlanan köprüleri, Pazar akşamüstü yürüyüşleri için kullanırmış. Yürüyüşleri esnasında kendileri için bir oyun tasarlamaya karar vermişler. Amaçları, şehrin etrafını dolaşırken her bir köprüden bir kez geçecek şekilde bir rota bulmakmış. Königsbergliler böyle bir izlek bulamasa da aralarından hiç kimse bu rotanın asla bulunamayacağını kanıtlayamamış.

Euler problem ile nasıl tanıştı?

1707 ile 1783 yılları arasında yaşayan İsviçreli matematikçi Leohard Euler, kaleme aldığı altmış ila seksen ciltlik külliyat ile insanlık tarihinin en üretken matematikçisidir. Bilim dünyasına adımlarını Basel Üniversitesi’nde atan Euler, on üç yaşında başladığı üniversite eğitimini, altı yıl sonra, İsviçreli bilim insanı Johann Bernolli’nin danışmanlığında yazdığı doktora tezi ile tamamlar. Paris Akademisi ve Büyük Prusya Berlin Akademisi’nde de çalışan Euler, ömrünün sonuna kadar St. Petersburg Bilimler Akademisi’nde çalışır.

Euler, Königsberg’te böyle bir rotanın bulunamayacağını, 1736’da, Commentarii Academiae Scientiarum Imperialis Petropolitanae isimli dergide yayımlanan Solutio problematis ad geometriam situs pertinentis başlıklı Latince makalede kanıtlar. Euler’in Königsberg köprüleri tasviri Şekil 3’de gösterildiği gibidir:

Euler’in St. Petersburg’da yazdığı makalesi yirmi bir maddeden oluşmaktadır ve bunlardan ilki şöyledir:

“Büyüklüklerle ilgilenen geometri dalı tarih boyunca aşk ile çalışılmıştır, ama konum geometrisi (geometri situs) olarak adlandırılan, ilk kez Leibniz tarafından dile getirilen, şu ana kadar neredeyse pek bilinmeyen başka bir dal var. Bu geometri dalı, yalnızca konuma bağlı ilişkilerle ilgilenir, konumun özelliklerini inceler; [ne] büyüklükleri hesaba katar, ne de nicelikler ile hesap içerir. Ama şimdiye dek, hangi problemlerin konum geometrisine ait olduğu ya da bu problemleri çözmek için hangi yöntemlerin kullanılacağına dair tatmin edici bir tanım verilmemiştir. Son dönemlerde, geometriye ait gibi gözükmesine karşın, bununla beraber [ne] bir büyüklüğün belirlenmesi olarak adlandırılabilecek ne de niceliksel hesap ile çözülebilecek şekilde hazırlanan bir problem duyuruldu; sonuç olarak, özellikle hesap kullanılmaksızın yalnız konumun izanını gerektirmesinden dolayı, bu problemin konum geometrsine ait olduğunu saptamakta tereddüt etmedim. Bu makalede, konum geometrisinin bir örneği olarak sunulabilecek bu tip bir problemi çözmek için keşfettiğim yöntemi açıklayacağım.”

Euler’in problemden nasıl haberdar olduğu bilinmiyor. Ancak Sovyetler Birliği Bilimler Akademisi Bülteni’nde (Izvestiia Akademii Nauk SSSR) yayımlanan, Euler’in St. Petersburg Bilimler Akademi’sindeki mektuplaşmalarını içeren Bilim İnsanlarına Mektuplar (Pis’ma k ucenyum) isimli makale, bu tarihsel muğlaklığa biraz olsun ışık tutuyor.

Bunlardan ilki, Königsberg’in yaklaşık seksen kilometre batısında yer alan Danzig şehrinin valisi Carl Leonhard Gottlieb Ehler ile arasındadır. Ehler, Euler ile yerel bir matematik profesörü olan Heinrich Kühn’e aracılık etmek için yazışır. Başlangıç konuşmaları günümüze ulaşamasa da 9 Mart 1736’ya tarihlenen mektupta problemi ve onun konum geometrisi ile ilişkisinin tartışırlar:

“Çok bilgili beyefendi, eğer bana ve arkadaşımız Kühn’e çok iyi bildiğiniz Könnigsberg’in yedi köprüsü probleminin çözümünü bir kanıt ile birlikte gönderirseniz, bizi en kıymetli hizmetinize fazlasıyla borçlu kılmış olursunuz. Sizin büyük dehanıza layık konum kalkülüsün (Calculi Situs) mükemmel bir örneği olarak kendini gösteriyor. Söz konusu köprülerin taslağını ekledim…”

Euler 13 Nisan 1736’ya tarihlenen yanıtında, probleme ve çözümüne ilgisiz kalır:

“… En soylu beyfendi böylece görüyorsunuz ki, bu tip bir çözüm matematikle küçük bir ilişki taşıdığı için, herhangi biri yerine neden bir matematikçinin çözümü üretmesini umduğunuzu anlamıyorum. Çözüm sadece mantıksal bir gerekçeye dayandığı için keşfi herhangi bir matematiksel ilkeye bağlı değildir. … Bu arada, en soylu beyefendi, soruyu konum geometrisi ile ilişkilendirmişsiniz, ama ben bu yeni disiplinin ne içerdiği ve hangi tip problemlerin Leibniz ve Wolff tarafından bu şekilde ifade edilmesinin umulduğu hususunda habersizim…”

Euler aynı zamanlarda, 13 Mart 1736’da, Viyana’da yaşayan İtalyan matematikçi ve mühendis Giovanni Marinoni’ye yazdığı mektupta problemi şu şekilde sunar:

“Königsberg şehrinde yedi köprünün üzerine yayıldığı bir nehirle çevrili bir ada hakkında bana bir soru yöneltildi ve birisinin her köprüden sadece bir kez geçecek şekildeki bağlantılı bir yürüyüşte, ayrı köprüleri geçebilir mi diye soruldu. Şimdiye kadar hiç kimsenin, bunu yapma olasılığını göstermediği veya bunun imkansız olduğunu gösterdiği konusunda bilgilendirildim. Bu soru çok bayağı, ama bana ne cebir, ne de sayma sanatı onu çözmek için yeterli olduğu için dikkate değer gözüktü. Bundan dolayı, Leibniz’in bir zamanlar çok fazla özlenimini duyduğu konum geometrisine ait olup olmadığını merak ettim. Ve böylece, biraz üzerine düşündükten sonra, basit ama tamamen belirlenmiş bir kural elde ettim, bunun yardımıyla birisi, herhangi şekilde düzenlenmiş herhangi bir sayıda köprüden oluşan bu tür tüm örneklerde, bu tip bir gidiş dönüşün mümkün olduğuna veya olmadığına hemen karar verebilir...”

Euler’in makalesi

Daha önce de bahsettiğimiz gibi Euler’in makalesi yirmi bir maddeden oluşuyor. Madde dokuzun sonunda Euler problemin çözümüne ulaşır. Bundan sonraki maddeler problemin genel halinin çözümüne odaklandığı için burada sunmayacağız.

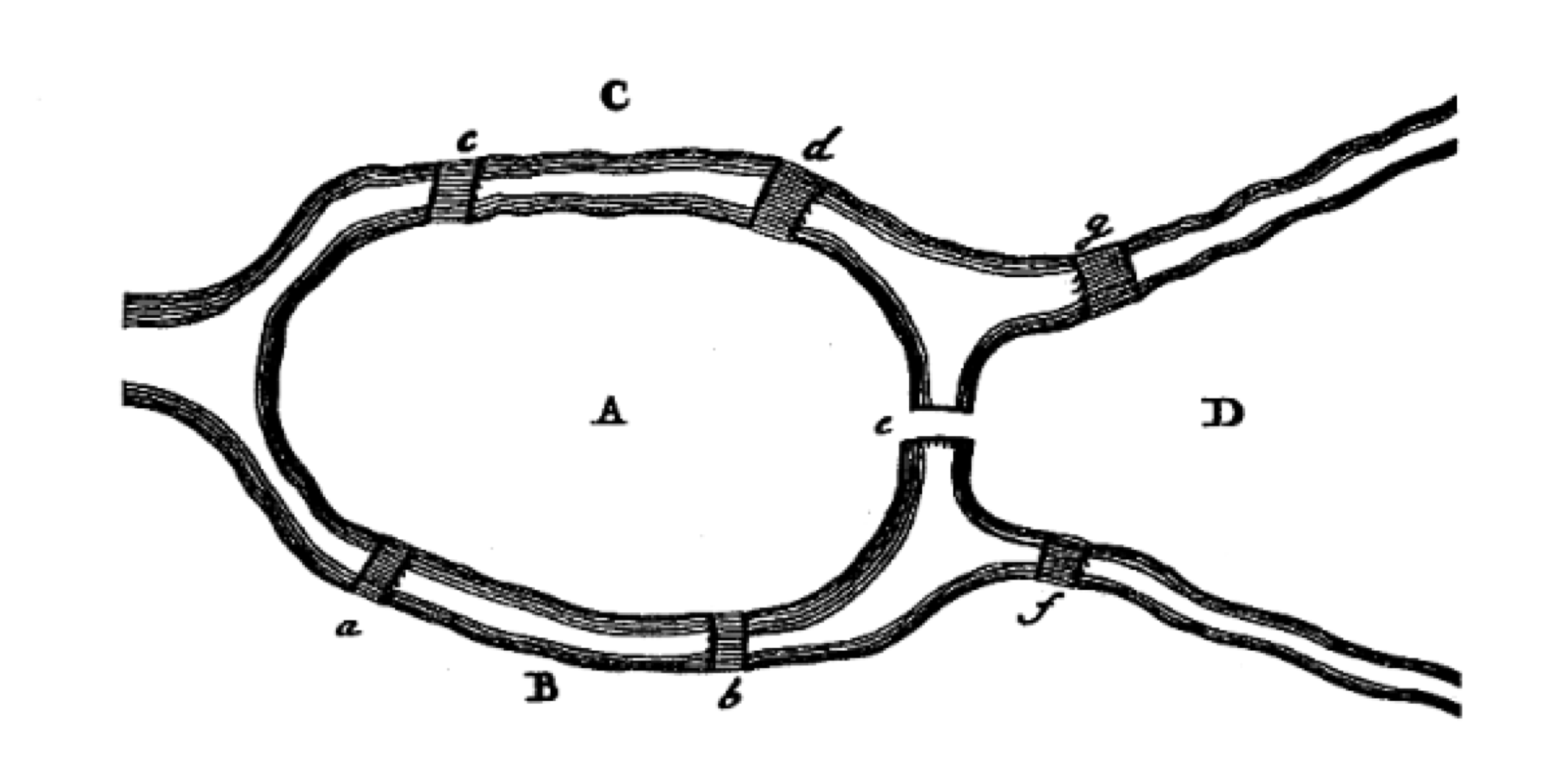
İkinci maddede Euler Könnigsberg’in yedi köprüsü problemini modeller. Şekil 1’de de göründüğü gibi, \( C\), \( D\) ve \( B\) sırasıyla, Pregel Nehri’nin üstünde, altında ve sağında kalan bölgeleri, \( A\) ise Kneiphof adasını tasvir ediyor. Sırasıyla, \( a\) ve \( b\) harfleri \( A\) ve \( B\) bölgelerini, \( c\) ve \( d\) harfleri \( A\) ve \( C\) bölgelerini, \( e\) harfi \( A\) ve \( D\) bölgelerini, \( f\)  harfi \( B\) ve \( D\) bölgelerini ve son olarak \( g\) harfi \( C\) ve \( D\) bölgelerini birbirine bağlayan yedi köprüyü adlandırmak için kullanır.

Üçüncü maddede Euler, bu problemin bütün olası rotaları dikkatlice tasnif edilerek çözülebileceğini dile getirmiş, ancak çok fazla sayıda kombinasyon ortaya çıkacağı için bu yöntemi çok sıkıcı ve zor olarak nitelendirir. Bu nedenle, çok daha basit olacağını umduğu bir yönteme yönelir.

Dördüncü ve beşinci maddede Euler yöntemini ortaya koyar: Eğer bir kişi \( A\) bölgesinden \( B\)’ye \( a\) ya da \( b\) köprüsünden geçerek ulaşırsa, bu geçişi \( AB\) olarak adlandırır. Benzer şekilde \( BD\), \( B\) bölgesinden \( D\) bölgesine \( f\) köprüsü ile geçisi temsil ediyor. Bu iki geçişin peşi sıra uygulanışını da \( ABD\) ile gösterir. Eğer benzer bir şekilde \( D\) bölgesinden \( C\) bölgesine \( g\) köprüsü ile geçersek \( ABDC\)’yi elde ederiz. Bu yöntemle Euler geçiş sırasını da akılda tutar ve genelleyerek sekiz harfin yedi geçişe karşılık geldiğini saptar.

Altıncı ve yedinci maddede Euler, geçişin birden fazla köprüyle sağlanabildiği durumlarda hangisini kullanarak geçiş yaptığını belirtmediğini vurgular. Königsberg köprülerinden geçerek oluşturacağımız bir rota köprülerden yalnız ve yalnız bir kez geçecek şekilde tasarlandığı için bu rotanın sekiz harften oluşacağını ve bu sekiz harflik kombinasyonun \( AB\) ve \( AC\)’yi iki kez içerirken, \( AB\), \( BD\) ve \( CD\)’yi bir kez içericeğini tespit eder. Son olarak Euler, problemin \( A\), \( B\), \( C\) ve \( D\) harflerinden oluşan sekiz harflik bir kombinasyonun analizine indirgendiğini dile getirir.  

Euler sekinci maddeye Şekil 6’te gösterilen basit durumu analiz ederek başlar. Eğer sadece bir köprü varsa ona \( a\) diyelim ve eğer bir kişi \( a\) köprüsünden geçmek üzereyse, ya geçmeden önce \( A\) bölgesindedir ya da geçtikten sonra \( A\) bölgesine varacaktır. Yöntemimize göre bu durumda, \( A\) harfi ifademizde yalnız bir kez ortaya çıkar. Eğer \( a\), \( b\) ve \( c\) köprüleri varsa ve bir kişi bunlardan geçecekse o zaman \( A\) harfi ifademizde iki kez yazılacaktır. O zaman \( A\)’yı üç kez yazıyorsak, beş köprümüz var demektir. Euler sonunda şu çıkarıma ulaşır: Köprü sayısı tek ise \( A\)’yı, bu tek sayıya bir ekledikten sonra ikiye bölerek elde edilen sayı kadar yazarız.

Dokuzuncu maddede Euler, Könnigsberg kentinde insanların var olmasını umduğu Pazar akşamüstü yürüyüş rotasının olamayacağını kanıtlamıştır: Böyle bir rotanın varolduğunu varsayalım. \( A\) adasından başlayan (ya da biten) \( a\), \( b\), \( c\), \( d\), \( e\) ile isimlendirdiğimiz beş farklı köprü var. Demek ki \( A\) üç kez yazılacak. Benzer şekilde \( B\), \( C\) ve \( D\) harfleri ikişer kez ortaya çıkacak. Sonuç olarak, \( A\) üç kez, \( B\), \( C\) ve \( D\) ikişer kez yazılmalıdır. Bu durumda dokuz tane harfe ihtiyacımız var, ama dördüncü ve beşinci maddenin sonunda sekiz harf ile yapabildiğimizi belirlemiştik. O zaman böyle bir rota oluşturmak imkansız!

Topolojinin Doğuşu

Fark ettiğiniz üzere Euler problem çözümünde ne Kneiphof adasının ne de diğer kara parçalarının yüz ölçümleri ile ilgilenmiyor. Köprülerin herhangi birinin uzunluğunu veya herhangi iki köprü arasındaki mesafeyi önemsemiyor. Euler için tek belirleyici şey, kara parçalarının birbirlerine göre konumlanışı ve kara parçalarınn bütünle ilişkisi olmuştur. Euler’in bu makalesi, Leibniz’in bir tür vektör kalkülüs olarak görülebilecek konum geometrisi çalışmalarınından, detaylı hesaplama içermemesinden dolayı farklılaştığı için, matematikçiler tarafından topolojinin ilk tarihsel izi olarak kabul görür.

Yunancada konum bilimi anlamına gelen topoloji, matematiğin, uzam veya şekil değişikliklerinden etkilenmeyen konum özellikleriyle ilgilenen dalıdır. Temel nesneleri, düğümler, yüzeyler ve manifoldlardır. Topolojik özellikleri tanımlamanın belki de en kolay yolu, gerilme veya bükülme gibi deformasyonlara rağmen aynı kalan geometrik özellikler olduklarını söylemektir. Örneğin, bir topolog, kahve bardağı ile donatı birbirinden ayıramaz!

Topoloji, bu deformasyonlar altındaki biçimsel tutarlılıkla ilgilenir, geometri ile arasındaki en temel niteliksel fark budur ve bu bağlamda geometrinin bir soyutlamasıdır.

Kaynaklar

Euler, L. - Solutio problematis ad geometriam situs pertinentis, Commentarii Academiae Scientiarum Imperialis Petropolitanae 8, 128-140, 1736, reprinted in Opera Omnia, Series 1, Volume 7, pp. 1 - 10, 1975.

Euler, L. - Pis'ma k ucenym, Izd. Akademii Nauk SSSR, Moscow-Leningrad, 1963.

Hopkins, B., Wilson, R. - The truth about Königsberg, College Math. J., 35: 198 - 207, 2004.

Newman, J. R. (ed.) - The World of Mathematics, Part 4.4, Vol. 1, Simon and Schuster, New York, 1956.

Görüş ve önerileriniz için: [email protected]