İnşa etmeden ispat
İstenilen özellikteki bir matematiksel kavramın varlığı, yokluğunun mantıksal imkansızlığıyla gösterilebilir: öyle iki \(a,b\) irrasyonel sayısı var mıdır ki \(a^b\) rasyonel olsun? Sorunun cevabının evet olduğunu böyle bir sayı çifti inşa etmeden göstermek te mümkün.
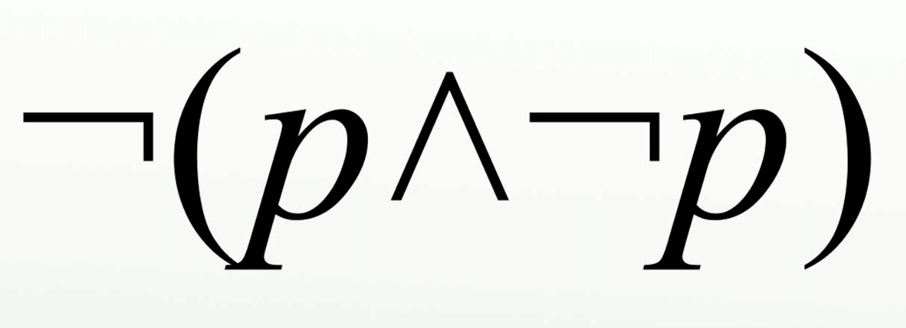
[BAA – Matematik]
Öncelikle, rasyonel sayı ve irrasyonel sayı kavramlarını kısaca tanıtmaya çalışalım. \(1,2,3,\ldots\) şeklinde ifade edilen sayılar kümesine doğal sayılar kümesi diyoruz. Bu sayıların negatiflerini (\(-1,-2,-3,\ldots\)) ve sıfırı doğal sayılar kümesine eklediğimizde tamsayılar kümesini elde etmiş oluyoruz. İki tamsayının bölümü şeklinde yazılan sayılara ise rasyonel sayılar kümesi diyoruz. Geometri bize her uzunluğun rasyonel bir şekilde ifade edilemeyeceğini söylüyor. Mesela, kenar uzunlukları 1 birim olan ikizkenar bir dik üçgenin hipotenüs uzunluğu Pisagor Teoremi yoluyla hesaplandığında \(\sqrt{2}\) elde ederiz: yani kendisiyle çarpımı 2 olan sayı. Bu sayının rasyonel olmadığı, yani iki tamsayının bölümü şeklinde yazılamadığı biliniyor. Bu türlü iki tamsayının bölümü olarak ifade edilemeyen niceliklere ise irrasyonel sayı diyoruz. Tanım gereği irrasyonel sayılar kümesi ve rasyonel sayılar kümesi birbirinden ayrık kümeler; yani bir sayı hem rasyonel hem de irrasyonel olamaz.
Cevaplamaya çalıştığımız soru şu: öyle iki \(a,b\) irrasyonel sayısı bulabilir miyiz ki, \(a^b\) sayısı rasyonel olsun? \(\sqrt{2}^\sqrt{2}\) sayısını ele alalım. \(\sqrt{2}\)’nin bir irrasyonel sayı olduğunu biliyoruz. Dolayısıyla, eğer \(\sqrt{2}^\sqrt{2}\) sayısı rasyonel ise istediğimizi elde etmiş oluruz.
Değilse, yani \(\sqrt{2}^\sqrt{2}\) sayısı irrasyonel ise, o zaman \(a=\sqrt{2}^\sqrt{2}\) ve \(b=\sqrt{2}\) alalım. Bu durumda \(a\) ve \(b\)’nin her ikisi de irrasyoneldir ve
\(a^b=(\sqrt{2}^\sqrt{2})^\sqrt{2})=\sqrt{2}^{\sqrt{2}\times\sqrt{2}}=\sqrt{2}^2=2 \)
rasyonel olur.
Sonuç olarak, yazının başında sorduğumuz sorunun cevabının evet olduğunu ispatlamış olduk. Yani verilen özelliği sağlayan \(a\) ve \(b\) sayı çifti vardır. Ancak ispatımızda, istenilen özelliği sağlayan bir sayı çifti inşa etmedik. Bu tür ispatlar matematikte inşacı olmayan ispatlar olarak bilinirler. Yani istenilen özellikte olan şeyin var olduğunu ispatlamış oluyoruz ancak o şeyi inşa etmeden.
Kaynaklar:
https://en.wikipedia.org/wiki/Law_of_excluded_middle