Bir dakikada matematik: Döşeme problemleri

Bir duvarı, tüm düzgün çokgenler arasında yalnızca üç tanesi ile döşeyebilirsiniz: kare, eşkenar üçgen ve düzgün altıgen. Diğerleri tam olarak birbirine oturmazlar.

[BAA – Matematik/ Çevirmen: Duygu Özdemir]

Tüm düzgün çokgenler arasında yalnızca üç tanesi ile bir duvarı döşeyebilirsiniz: kare, eşkenar üçgen ve düzgün altıgen. Diğerleri tam olarak birbirine oturmazlar.

Bunu kanıtlamak oldukça kolaydır. \( n \) kenarlı bir düzgün çokgen  

\( 180 \frac{n-2}{n} \)  

derecelik iç açılara sahiptir. Bir noktanın etrafına bir çokgenin birçok kopyasını, onlara \( k\) diyelim, tüm kenarlar buluşacak şekilde yerleştirip döşeme yapmayı denediğinizi varsayalım (aşağıdaki görsele bakabilirsiniz). O zaman \( k\) tane açının toplamı \( 360\) derece olmalıdır. Eğer daha az eklenirse bir boşluk oluşacaktır, eğer daha fazla eklenirse çokgenin kopyaları üst üste bineceklerdir.

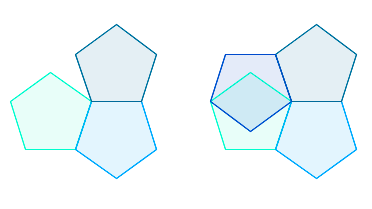
O halde ihtiyacımız olan  

\( k \times  180 \frac{n-2}{n} = 360\),  

bu da şu demek

\( k = \frac{2n}{n-2} \).  

Eşitliğin sağındaki terimi tekrar yazarsak şu sonucu verir  

\( k = \frac{4}{n-2} +2 \).

\( k \) bir tam sayı olduğu için (birbirine oturtmaya çalıştığımız çokgenin kopyalarının sayısı), \( \frac{4}{n-2} \) de bir tam sayı olmalıdır. Dolayısıyla \( n-2 \) yalnızca \( 4 \), \( 2 \) ve \( 1\)’e eşit olabilir. Bu da \( n \) yalnızca \( 6 \), \( 4 \) ve \( 3\)’e eşit olabilir demek.

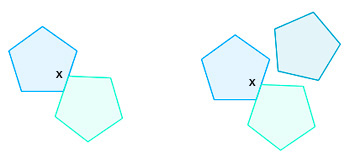
Aynı zamanda çokgendeki bir köşenin her zaman komşu kopyanın bir köşesi ile buluşmasına gerek olmadığı ama komşu kopyanın \( x \) uzunluğundaki kenarında bazı noktalara oturduğu bir döşeme yapmak için şunu da deneyebilirsiniz. Bu komşu kopya ayrıca \(x\)’e bağlı \( 180 \) derecelik bir iç açıya sahip olacaktır ( \( x\), kenarların birinin iç kısmında olduğunda). Bir döşeme yapmak için kalan \( 180 \) derecelik \( k \) kadar çokgen kopyasını doldurmanız gerekecektir, yani şuna ihtiyacınız olacaktır  

\( k \times  180 \frac{n-2}{n} = 180\).

Yukarıdakine benzer bir argümanla bunun yalnızca \( n=3 \) ya da \( n=4 \) olduğunda işe yaradığına kendinizi ikna edebilirsiniz.

Kaynak:

Plus Magazine, Maths in a minute: Tiling troubles, https://plus.maths.org/content/maths-minute-tiling-troubles