SSCB’de Topoloji (1917-1958)

İnsanlığın çetin sınıf mücadeleleri sonucunda var ettiği ilk işçi devleti olan Sovyet Sosyalist Cumhuriyetler Birliği'nde, bilimin tüm alanlarının kolektif ve planlı iş bölümüyle örgütlenmesi sayesinde inanılmaz bir tarihsel ilerleme yaşandı. Tüm bilimsel yelpazenin içerisinde matematik bu sıçramadan en çok nasibini alan bilimlerden birisiydi. Matematiğin tamamını bir kenara bırakın sadece belirli bir alan merkeze alınsa bile, bir makale dizisinde mevcut üretimin tümünü ele almak imkansız bir uğraştır. Tam da bu sebeple, topoloji alanındaki önemi evrensel olarak da tescillenmiş kimi sonuçlara odaklanarak ilerleyeceğiz ve temel amacımız Sovyet topolojisini modern matematiksel bilgilerle harmanlayarak sunmak olacak.

Sovyet Sosyalist Cumhuriyetler Birliği'nde matematiği kavrayışa dair fikir vermek için döneme yön veren ünlü Sovyet matematikçi A.N. Kolmogorov'un, Büyük Sovyetler Ansiklopedisi'ne yazdığı matematik maddesine göz atalım. Burada Kolmogorov matematiği diyalektik materyalist perspektif ile Engels'i referans göstererek şöyle tanımlıyordu: "Matematik, gerçek dünyanın niceliksel ilişkilerinin ve uzaysal şekillerinin bilimidir" (Mathematics, GSE, 1970-1979). Kuşkusuz ki bu tanım modern matematiği anlamlandırmak için eksiktir ancak diyalektik materyalist yöntemin doğası gereği gelişime açıktır. Bu uğraş bambaşka bir yazının konusu olmaya aday olmakla birlikte, belirtmeliyiz ki, bu haliyle bile diğer idealist felsefi yaklaşımların aksine matematiğin yeryüzüyle ilişkisine dair kıymetli bir perspektif sunmaktadır ve geçerliliği ve gücü günbegün kanıtlanmaktadır. Bugünkü yazımızın konusunu oluşturan topoloji alanına dönecek olursak, Yunanca kelime kökenin de anlaşılabileceği üzere konum bilimi manasına gelir ve matematiksel uzayların sürekli deformasyonlar altında değişmemesini referans alarak matematiksel uzayları ilişkileriyle birlikte kavramaya, analiz etmeye ve sınıflandırmaya çalışır.

Matematik tarihi içerisinde topolojinin doğuşunu müjdeleyen ilk çalışma, matematikçiler arasında yaygın bir şekilde kabul de gördüğü üzere, Leonard Euler'e aittir (Euler, 1741). Dönemin Prusya'sında yer alan Königsberg'de, rivayete göre insanlar şehrin yedi yerine konuşlanan köprüleri, Pazar akşamüstü yürüyüşleri için kullanırmış. Königsberg'in yedi köprüsü problemine de şu soru kaynaklık ediyor: Şehri dolaşırken her bir köprüden bir kez geçecek şekilde bir rota bulunabilir mi?

Böyle bir rotanın çizilemeyeceğini kanıtlayan Euler Königsberglileri üzerken, matematiğin içinde artık geometriden farklılaşan bir alanın var olduğuna işaret ediyordu. Çünkü problemin çözümünde ne adanın ne de diğer kara parçalarının yüz ölçümleri ile ilgilenilmez. Bunun yanı sıra köprülerin herhangi birinin uzunluğu veya herhangi iki köprü arasındaki mesafe önem arzetmez. Tüm bunların yerine tek belirleyici şey, kara parçalarının birbirlerine göre konumlanışı ve kara parçalarınn bütünle ilişkisi olmuştur. Yani problemin çözümünde niceliksel büyüklüklerden ziyade niteliksel özellikler belirleyici olmuştur (Şavk, 2019a).

Yine Euler topolojinin öncül makalelerinden bir diğerinde düzgün içbükey çokyüzlüler için önemli bir değişmez bulmuştur (Euler, 1758) [1]. Çokyüzlünün köşe sayısını \(V\), kenar sayısını \(E\) ve yüz sayısını \(F\) ile gösterirsek, Euler'in meşhur çokyüzlü formülü şu şekildedir:

$$V - E + F = 2.$$

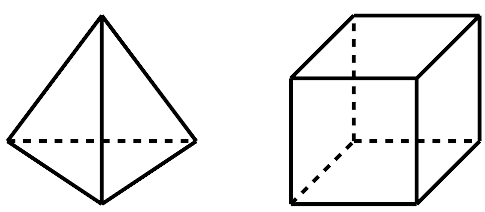
Bu yaklaşım daha sonraları tüm topolojik uzaylara genişletilecek ve bugün topolojik uzayların en önemli değişmezlerinden biri olan homolojinin ve dolayısıyla Euler karakteristik değişmezi olarak bilinen niceliğin en büyük esin kaynağını oluşturacaktır. Euler'in argümanı bazı çokyüzlüler doğru olmayacak şekilde kurulduğu için kanıtında bir açık bulunmuş ve akabinde A.M. Legendre tarafından geçerli bir ispat verilmiştir (Şavk, 2019b, 2019c).

Euler, Sovyet toprakları için çok önemli bir bilimsel figürdür çünkü ömrünün çok büyük bir bölümünü en derin bilimsel gelişmelerini ortaya koyduğu St. Petersburg Bilimler Akademisi'nde çalışarak geçirmiştir. Büyük matematikçilerden biri P.S. de Laplace'a göre Euler onsekizinci yüzyılın ikinci yarısının matematikçilerinin öğretmeni ve yol göstericisidir. Çalışmalarıyla Laplace'ın kendisi başta olmak üzere, Lagrange, G. Monge, A. M. Legendre ve Gauss ve daha sonra A. Cauchy, M.V. Ostrogradskii ve P.L. Chebyshev gibi matematikçilere ve dolayısıyla dünya matematiğine yön vermiştir (Euler, GSE, 1970-1979).

Bu noktadan itibaren, yazımızın tarihsel arka planını yerli yerine oturtmak ve batı kaynaklı makalelerin sınırlı ve Sovyet matematiğinin kayda değer bir kısmını yok saydığı bilgi akışının ve paylaşımının dışında kalmak için A.D. Aleksandrov'un SSCB'deki geometri ve topolojinin ilk otuz yılını en derin ayrıntısına kadar ele aldığı yazı dizisinin ilkini takip edeceğiz (Aleksandrov, 1947).

Matematik literatüründe, topoloji terimi 1847'de Gauss'un öğrencisi Alman matematikçi J.B. Listing tarafından ortaya kondu; alana dair diğer bir isim, analysis situs idi, 1857'de Riemann tarafından cebirsel fonksiyonlar teorisi üzerine yaptığı çalışmada kendini gösterdi. Bu çalışmaları bugün Möbius şeridi olarak bildiğimiz tek taraflı ve kenarlı yüzeyi ortaya koyan Alman matematikçi A.F. Möbius takip etti.

Topolojinin kendi kavramları, yöntemleri ve problemleri ile bağımsız bir disiplin olarak varolması Fransız matematikçi Henri Poincaré'nin ondokuzuncu yüzyılın son yıllarındaki çalışmalarıyla mümkün oldu. Poincaré'nin araştırmasının merkezinde topolojik politoplar, yani \(n\)-boyutlu bir Öklid uzayının topolojik görüntüleri olarak ele alabileceğimiz, sonlu veya sayılabilir sayıda topolojik simplekse ayrıştırılabilen uzaylar yer alıyordu. Bu uzaylar çokyüzlülerin üçüncü boyuttan herhangi bir boyuta genellenmesidir. Bu simpleksleri birleştirerek elde edilen simpleksler kompleksi yapısının üzerine cebirsel ifadeler atayarak günümüzde homoloji olarak adlandırdığımız kavramı ortaya koydu.

Kuşkusuz ki topoloji alanının ondan tarihsel olarak da eski olan analiz alanıyla derin ilişkileri bulunmaktadır. Bu alanın temel çalışma nesneleri olan fonksiyon uzayları, ilk olarak 1904'te Fransız matematikçi M.R. Fréchet ve ardından 1914'te Alman matematikçi F. Hausdorff tarafından çalışıldı. Topolojik uzay kavramları fonksiyon uzaylarına soyutlandı ve bu sayede analitik nesnelerin sınır, bağlantı, vb. özellikleri ele alındı.

Genel topolojinin cebirsel topoloji ile birleştirilmesinin temelini ise Hollandalı matematatikçi L.E.J. Brouwer'in  1910-1912 yılları arasındaki çalışmalarına borçluyuz. Sürekli eşlemelerin, hafif deformasyonlardan sonra parçalı eşleme ile yaklaştırılabilmesini sağlayan, simpleksler yaklaşımı kavramını ortaya koydu. Bu sayede Brouwer bir dizi temel teoremi kanıtladı. İlki boyut değişmezliği teoremidir: eğer bir politop topolojik olarak bir diğerine eşlenirse [2], o zaman her iki politop da aynı boyuta sahiptir. Bu sonuçlardan bir diğeri ise bölgenin değişmezliği teoremidir: eğer \(n\)-boyutlu Öklid uzayının bir açık kümesi \(U\) , yine \(n\)-boyutlu Öklid uzayında başka bir \(V\) kümesine topolojik olarak eşlenebilirse, o zaman \(V\) kümesi de açıktır. Son olarak ise meşhur sabit nokta teoreminden bahsedebiliriz: Öklid uzayı içerisindeki \(n\)-boyutlu diskten \(D^n\) kendisine yazılabilen her sürekli dönüşümün en az bir sabit noktası vardır.

Sovyet topolojisi sahneye çıkmadan hemen önceki en derin sonuçlardan birine ise Amerikalı matematikçi J.W. Alexander imza atmıştır. Bunlardan ilki 1915 yılına ait meşhur Alexander ikilik teoremidir: Bu sonuç sonrasında cebirsel topoloji kısmında bahsedeceğimiz gibi Sovyet topolojiciler tarafından geliştirilmiş ve genellenmiştir.

GENEL TOPOLOJİ

1920'li yılların başlarından itibaren Sovyet genel topolojisinin kurucuları ve topoloji alanının dünya çapında sürdürücüleri P.S. Aleksandrov, L.S. Pontryagin, A.N. Tikhonov ve P.S. Uryhson [3]  ve öğrencileri oldular. Bu bilim insanlarının öncülüğünde, günümüzde topolojik uzaylara dair bildiğimiz bir dizi temel kavram yerli yerine oturtuldu ve bir çok yeni sonuç elde edildi.

Sovyet topolojisinin bu güçlü sanheneye çıkışı, tarihte yapılacak ilk uluslararası konferansın, Birinci Uluslarası Topoloji Konferansı'nın, şaşırtıcı olmayacak şekilde, 1935'te Moskova'da düzenlenmesine gerekçe oluşturdu.

Üzerinde net bir konsensüs olmamakla birlikte konferansta 45 konuşmanın verildiği düşünülüyor. Bunlardan 13 tanesi Sovyet matematikçiler P.S. Aleksandrov, N.N. Bogolyubov, N.M. Krylov, N.K. Brushlinskii, V.A. Efremovich, I.I. Gordon, A.N. Kolmogorov, A.A. Markov, V.V. Nemytskii, L.S. Pontryagin, J.A. Rózaáska, A.N. Tikhonov; 10 tanesi Amerikalı matematikçiler J.W. Alexander, G. Birkhoff, E.R. van Kampen, S. Lefschetz, J. von Neumann, P.A. Smith, M.H. Stone, A.W. Tucker, H. Whitney; 7 tanesi Polonyalı matematikçiler K. Borsuk, K. Kuratowski, S. Mazurkiewicz, J. Schauder, W. Sierpiński; 4 tanesi İsviçreli matematikçiler H. Hopf, G. de Rham; 3 tanesi Hollandalı matematikçiler D. van Dantzig, H. Freudenthal, W. Hurewicz; 2 tanesi Fransız matematikçi A. Weil; 2 tanesi Çekoslavakyalı matematikçi E. Čech, 2 tanesi Danimarkalı matematikçi J. Nielsen; 1 tanesi Alman matematikçi G. Nöbeling ve 1 tanesi Norveçli matematikçi P. Heegaard tarafından veriliyor (Lapko-Lusternik, 1957)[4]

Bugün lisans müfredatlarının içeriğine kadar indirilmiş, topoloji ve topolojiyle yakınen ilgili derslerin içerikleri neredeyse tamamen bu matematikçilerin sonuçlarıyla bina ediliyor. Bu sebeple makalede Sovyet topolojicilerinin genel topolojideki tüm sonuçları vermekten kaçınıp [5], onun yerine en önemlilerinden biri olarak bulduğum tek bir kavrama odaklanacağız: Aleksandrov'un tek-nokta kompaktlaştırması. Bu noktadan itibaren bu kavramının önemini ve derinliğini açıklamaya gayret ederek, en temel geometrik ve topolojik uzayların bir diğerinden bu yöntemle nasıl elde edildiğini sunmaya çalışacağız.

İlk olarak, topolojik uzayı sezgisel olarak kavramakla başlayalım. Geometrik uzayların aksine, topolojik uzaylarda noktalar arasındaki mesefeler sayısal bir büyüklük ifade edilip ölçülmese de kontrol edilir, yani bir noktanın etrafındaki komşuluğa ve noktaları içeren komşuluklar arasındaki ilişkilere odaklanılır. Bu manada topolojik uzaylar, geometrik uzayların matematiksel olarak bir soyutlamasıdır.

Daha formel bir şekilde ifadece olursak, topolojik uzaylar en yaygın biçimde açık kümeler vasıtasıyla tanımlanırlar. Şimdi \(X\) bir küme ve \( \tau\), \(X\)'in alt kümelerini içerek bir koleksiyon olsun. Aşağıdaki üç şartı sağlayan (\(X, \tau\)) ikilisine topolojik uzay diyoruz:

(1) Boş küme \(Ø\) ve \(X\), \( \tau \)’da yer alır.
(2) \(\tau \) ’nun içindeki kümelerin herhangi bir birleşimi yine \(\tau \)’nun içindedir.
(3) \(\tau\) ’nun içindeki kümelerin sonlu sayıdaki kesişimi yine \(τ\) ’nun içindedir.

(\(X,\tau\)) topolojik uzayının bir tabanı \(\beta \subset \tau \) bir alt koleksiyondur öyle ki \( \tau \)'nun herhangi bir elemanı \( \beta \)'nın elemanlarının birleşimi olarak temsil edilebilir. \( \tau \)'nun içinde yer alan her kümeye açık küme, tümleyeni \( \tau \)'da açık küme olan kümelere ise kapalı küme diyoruz. Kompaktlık kavramı da topolojik uzayları kendisi sonsuz olsa bile sonlu adet parçasına bakarak kavrayabilir miyiz fikrinden meydana geliyor. Birleşimleri tüm \(X\) kümesini veren açık kümelerin koleksiyonuna örtü diyoruz. Örtüler pekala sonlu ya da sonsuz tane kümenin birleşiminden oluşabilir. O yüzden eğer \(X\)'in her örtüsüne karşılık gelen sonlu bir alt örtü bulabiliyorsak \(X\)'e kompakt diyoruz. Örneğin, bu yaygın tanımı yine Sovyet matematikçiler Aleksandrov ve Uryshon'a borçluyuz [6] (Aleksandrov-Uryshon, 1929).

Şimdi Aleksandrov'un 1924'te ortaya koyduğu tek-nokta kompaktlaştırması kavramına geri dönelim (Aleksandrov, 1924). Adından da tahmin edilebileceği üzere bu kavram sayesinde kompakt olmayan bir uzaya sadece bir nokta ekleyerek kompakt bir uzay elde ediyoruz. Biraz daha açacak olursak, uzayın her bir noktasını içeren ve topolojik uzayın içinde yer alan bir açık kümeden bahsedebiliriz. Aleksandrov sayesinde başladığımız uzayda keyfi olarak aldığımız, açık kümelerden oluşan ve uzayı kaplayan herhangi bir örtünün sonsuz alt örtüsünü bulamazken, ona sadece sonsuzda bir nokta ekleyerek artık bunu mümkün kılmış olduk. Bu kavram, karşıtların birliği ilkesinin kendini berrak bir şekilde gösterdiği, sonlu-sonsuz diyalektiğine içkindir. Dolayısıyla Aleksandrov'un yöntemi, sonsuzda nokta ekleyerek veya başka bir deyişle sonludan sonsuza kaçışı önleyerek uzaydaki diğer noktaların sonsuzluğa gidişini kontrol etmeyi mümkün kılar.

Bir topolojiyi tarif etmek için onun açık kümelerini tarif etmemizin yeterli olduğunu söylemiştik. Şayet (\(Y, \tau_Y\)) topolojik uzayı aşağıdaki iki şartı sağlıyorsa, (\(X,\tau\)) topolojik uzayının Aleksandrov tek-nokta kompaktlaştırması olarak adlandırılır:

(1)  \(Y = X \cup \{\infty \} \)
(2)  \(\tau_Y = \{ U  |  U \in  \tau_X \} \cup  \{ Y \setminus F \ \vert \ F, X\text{’de kapalı} \} \).

Şimdi Öklid uzayıyla kürelerin arasındaki sıkı topolojik ilişkiyi Aleksandrov tek-nokta kompaktlaştırması vasıtasıyla ele alacağız. Bir \(n\)-boyutlu küre \(S^n\), orijinden birim uzaklıkta bulunan \((n + 1)\) boyutlu Öklid uzayı \(\mathbb{R}^{n+1}\)'deki noktalar kümesi olan topolojik bir uzaydır:

Bu tanım vasıtasıyla geometrinin temel nesneleri olan birim çemberi \(S^1\) ve birim küreyi \(S^2\) olan herhangi bir boyuta genellemiş olduk. Heine-Borel Teoremi Öklid uzayındaki kompakt kümeleri tamamen karakterize eder: bir kümenin kompakt olması için gerek ve yeter koşul onun kapalı ve sınırlı olmasıdır. \(S^n\) kapalıdır çünkü \(S^n\)'nin dışında aldığımız bir noktanın koordinatlarını yeterince küçük bir biçimde oynatırsak yine \(S^n\)’nin dışında kalırız ki, bu da \(S^n\)’nin dışının açık, kendisinin kapalı olduğunu gösterir. Sınırlı olduğu ise tanımı gereği açıktır, dolayısıyla \(S^n\) kompakt bir topolojik uzaydır. Ancak Öklid uzayını sınırlayamadığımız için kompakt olmadığını gözlemleyebiliriz. Şimdi ana argümanızı ifade edip sonra da onu açıklayama çalışalım:

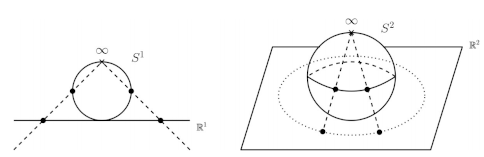
Teorem 2.1. Herhangi bir boyuttaki birim küre aynı boyuttaki Öklid uzayının bir Aleksandrov tek-nokta kompaklaştırmasıdır yani \(S^n = \mathbb{R}^n ∪ \{ \infty \} \).

Şimdi bu teoremin neden doğru olduğunu sezgilerimize de yaslanarak, geometrik bir argümanla ele alalım. Aşağı şekilde de görüldüğü gibi \(1\)-boyutlu Öklid uzayını \(\mathbb{R}^1\) topolojik olarak bir doğru parçası gibi düşünebiliriz çünkü uzatmak veya kısaltmak bir uzaydan diğerine bir homeomorfizma verir yani topolojisini korur. Şimdi bu doğru parçasını sonsuzdaki noktaya doğru ovalleştirebiliriz, hala \(\mathbb{R}^1\)'in homeomorfizma tipini koruyoruz. Son olarak sonsuzdaki noktayla iki ucunu birleştirerek birim çemberi \(S^1\) elde ederiz. Bu argümanı yine şekilde görüldüğü üzere iki boyutta da tekrarlayabiliriz.

Kompaklaştırma olgusu karşıtı olan dekompaktlaştırma olgusuyla birlikte varolur. Yani kompakt nesneden bir nokta çıkararak kompakt olmayan nesneyi geri edle edebiliriz. Bizim örneğimizde, bu olgu matematiksel olarak stereografik izdüşüm olarak bilinen, gündelik hayatta ise haritalamaya karşılık düşen yönteme karşılık gelir. Şayet nesnemizden sonsuzdaki noktaya karşılık gelen kuzey kutup noktasını genelliği bozmadan çıkarıp, o noktayı küre ve Öklid uzayından geçecek şekilde doğrularla izdüşürürsek süreci tamamlamış oluruz.

Tarif ettiğimiz kavram setiyle birlikte teoremimizi matematiksel olarak açıklayalım ve ilk olarak \(\mathbb{R}^1\) üzerindeki doğal topolojiden bahsetmekle başlayalım. Bunu yapmak için onun doğal tabanından bahsetmek yeterli olacaktır. Tahmin edilelebileceği üzere bu taban gerçel sayılar üzerindeki açık aralıklarla verilebilir. Genel olarak \(n\)-boyutlu Öklid uzayı \(\mathbb{R}^n\)'i aşağıdaki gibi düşünebiliriz:

Beklendiği üzere \(\mathbb{R}^n\)'e karşılık gelen topolojiyi \(\mathbb{R}\) üzerindeki topoloji vasıtasıyla elde ederiz: \(\mathbb{R}^n\) üzerindeki Tikhonov çarpım topolojisinin açık kümeleri, açık kümelerin çarpımı ve bu çarpımların olası birleşimleridir. Dolayısıyla \(R^n\)'e karşılık gelecek doğal taban, \(r \in \mathbb{R}^n\) ve \(\epsilon > 0\) olmak üzere, \(\beta_{r, \epsilon} = \{ \mathbf{x} \in \mathbb{R}^n \ : \ \vert \vert \mathbf{x} - r \vert \vert < \epsilon \} \)'dur. Şimdi \(\mathbb{R}^n\)'in Aleksandrov tek-nokta kompaklaştırmasına gelen \(\mathbb{R}^n \cup { \infty }\) topolojik uzayının bazını tarif edelim. Bunu da hali hazırda olan doğal taban \(\beta_{r, \epsilon}\)'u kullanarak ve sonsuzdaki noktanın açık komşuluğunu yazarak yaparız: \(R \in \mathbb{R}^n\) olmak üzere \(\beta_{\infty, R} = \{ \mathbf{x} \in \mathbb{R}^n \ : \ \vert \vert \mathbf{x}\vert \vert > R  \} \cup \{ \infty \}\). Özetle, \(\mathbb{R}^n \cup { \infty }\)'nin bazı \(\beta_{r, \epsilon}  \cup \beta_{\infty, R}\)'dir. Gösterilebilir ki bu uzay \(S^n\)'ye homeomorfiktir.

Aleksandrov'un tek-nokta kompaktlaştırması, Tikhonov'un da çalışmalarının üzerine bina edilerek Stone-Čech kompaklaştırmasıyla genellenmiştir. Hemen akla ilk gelebilecek başka bir yöntem de doğrudur: bir topolojik uzaya birden fazla nokta ekleyerek de onu kompaktlaştırabiliriz. Örneğin, gerçel ve karmaşık projektif uzaylar \(\mathbb{RP}^n\) ve \(\mathbb{CP}^n\), sırasıyla \(\mathbb{R}^n\) ve \(\mathbb{C}^n\)'nin bu manada kompaktlaştırmasıyla elde edilebilir.

CEBİRSEL TOPOLOJİ

Manifold tekil noktaları olmayan [7] bir eğri veya yüzey kavramının herhangi bir boyuta sadeleştirilerek genellemesiyle oluşan matematiksel nesnedir. Sadeleştirmekten kastımız tekilliklerden kurtulan geometrik nesnenin her noktasının civarının yerel olarak Öklid uzayına benzemesidir: Bu civara bir büyüteç ile yaklaştığımızı düşünelim. O noktanın etrafını çevreleyen bir komşuluğa baktığımızda Öklid uzayının bir kopyasını görmek istiyoruz; yani üzerinde geometri ve analiz yapmayı hali hazırda bildiğimiz en basit uzayı talep ediyoruz. Benzemeyi matematiksel olarak kavramlaştıracak olursak, her komşuluk ile Öklid uzayı arasında homeomorfizma adını verdiğimiz kendisi ve tersi birebir, örten ve sürekli bir fonksiyon yazıyoruz. Ancak genelleştirirken de manifoldun bütününde herhangi bir karmaşıklığa izin verişimiz yapımıza zenginlik katıyor: Bu serbestlik bize Öklid uzayından başlayan geniş bir uzay yelpazesi sunuyor. Bir manifoldun boyutuna ise yerel olarak karşımıza çıkan Öklid uzayının boyutuna bakarak karar veriyoruz. Dolayısıyla yerel olarak \(\mathbb{R}^n\) Öklid uzayına benzeyen bir \(M\) topolojik uzayı \(n\)-boyutlu manifoldtur, kısaca \(M\)'ye \(n\)-manifold diyelim.

Bu parça-bütünlük diyalektiğine dair hassas ve derinlikli soyutlama, geometrinin birçok temel nesnesine yeni ve farklı bir perspektiften bakmamıza olanak sağlıyor. Manifold kelimesinin etimolojik kökeni bu soyutlamanın felsefesine dair derin izler taşıyor. Üstelik dönemin matematiksel bilgi birikiminde meydana gelen sıçramayı gözlemlememize de olanak sağlıyor. Sanılanın aksine manifold sözcüğü İngilizce many ve fold kelimelerinin birleşiminden değil, Türkçeye aynı zamanda çeşitlilik/varyete olarak da çevirebileceğimiz Mannigfaltigkeit isimli Almanca sözcükten türetilmiştir ve ilk olarak Bernhard Riemann tarafından kullanılmıştır (Riemann, 1851) [8]. Bu tarihsel ana kadar matematikçiler için biricik geometri, Öklid’in düz geometrisi olagelmiştir. On dokuzuncu yüzyılın ikinci çeyreğinden itibaren J. Bolyai, N.I. Lobachevski, C.F. Gauss ve B. Riemann gibi matematikçilerin çalışmalarıyla inşa edilen Öklid dışı geometriler, Öklid geometrisinin biricikliğini nihai bir biçimde ortadan kaldırmıştır. Bu sarsıcı geçiş maddi dünyayı materyalist bir biçimde kavramanın bir ürünüdür ve bu kırılma, sarsıntılı geçiş fizik bilimindeki Newton fiziğinden Einstein fiziğine geçiş ile kıyaslanabilir. Arap matematiğindeki çürütme girişimlerini bir kenara koyacak olursak, iki bin yıldan fazla bir süre kimse Öklid geometrisinin doğruluğundan şüphe etmedi, sarsılmaz otoritesini sorgulamadı veya ona bir alternatif bulmayı düşünmedi. Ünlü matematik tarihçisi Kline (1990)'ın bu alt üst oluş hakkındaki cümlesini anımsatalım: "Öklid dışı geometrinin yaratılması, Yunan zamanlarından beri matematikte en önemli ve devrimci adımdı."

Manifoldlar Poincar'e'nin çalışmalarından itibaren topolojinin ve genel olarak matematiğin içersinde ciddi bir yer tutmuşlardır. Yazımızın bundan sonraki bölümü, Poincar'e ikiliğinden başlayarak manifoldlara karşılık gelen cebirsel nesneler olan homoloji ve kohomoloji grupları değişmezlerinin arasındaki sıkı ilişkiyi açıklamaya çalışan, ikilik teoremlerine odaklanacak. Sırasıyla, Poincar'e, Alexander, Pontryagin ve Sitnikov ikilik teoremlerini sunacağız ve Pontryagin İkiliği'nin kökenini ele alacağız.

Teorem 3.1 (Poincaré İkiliği, Poincaré, 1893). \(G\) bir abel grup, \(M\) kapalı, yönlendirilmiş bir \(n\)-manifold olsun. O zaman \(M\)'nin \(k\) dereceden homoloji grubuyla \((n-k)\) dereceden kohomoloji grubu birbirine izomorfiktir. Yani \(H_k(M;G) \cong H^{n-k}(M;G)\).

Yukarıdaki teoremin ifadesi Poincaré'nin tarafından, Betti grupları üzerinden daha cebirsel bir şekilde ifade edilmiştir. 1930'lu yıllarda, topolojik uzayların kohomoloji teorisi Aleksandrov, Kolmogorov ve Čech tarafından ortaya konmasıyla birlikte Čech ve Whitney bu yapının üzerinde, bir gruptan fazla olarak bir halka yapısı kurulabileceğini fark etmişlerdir. Kohomoloji halkası üzerinde kap ve kep çarpım ortaya konduktan sonra Poincaré İkiliği, yukarıdaki modern formulasyonuna kavuşmuştur.

Manifoldlar üzerinde bu netlikteki bir sonuçtan itibaren ikilik teoremleri, en genel olarak herhangi bir topolojik uzayda, içinde yer alan bir alt kümenin karakterizasyonuyla birlikte çalışılmıştır. Bu sayede topolojik uzaylara karşılık gelen cebirsel değişmezler göreli olarak incelenmiştir.

Bir sonraki ikililiğe geçmeden önce topolojik uzaylar için epey önemli bir yer tutan büzülme olgusuna göz atalım. Sezgizel olarak bir noktaya sürekli bir biçimde büzebildiğimiz topolojik uzaylara büzülebilir uzay diyoruz. Matematiksel bir şekilde ifade edecek olursak topolojik uzayımızın birim dönüşümünün bir sabit dönüşüme homotopik olmasıdır yani sıfır anında birim dönüşüm, bir anında sabit bir dönüşüme karşılık gelecek, uzayın kendisinin birim aralıkla kartezyeninden kendisine sürekli bir dönüşüm bulmamız gerekir. Şayet uzayımızın her noktasındaki komşuluk böyle davranıyorsa yerel büzülebilir uzay diyoruz [9]. Şimdi Alexander ikiliğini ifade edebiliriz.

Teorem 3.2 (Alexander İkiliği, Alexander, 1915). \(G\) bir abel grup ve \(A\), \(S^n\)'in kompakt, yerel büzülebilir bir alt uzayı olsun. O zaman \(A\)'nın \(S^n\)'deki tümleyenin indirgenmiş \(k\) dereceden homoloji grubuyla kendisinin \((n-k-1)\) dereceden kohomoloji grubu birbirine izomorfiktir. Yani \(\tilde{H}_k(S^n \setminus A ;G) \cong \tilde{H}^{n-k-1}(A;G)\).

Klasik homoloji teorisinde ortaya çıkacak patolojileri, topolojik uzayımızı simpleksler kompleksi haline getirirken, örtülerin arasındaki kesişimleri hassas bir şekilde kontrol ederek ve rafine ederek, ortadan kaldırabiliriz. Bu şekilde ortaya konan cebirsel teorilere Aleksandrov-Čech homoloji ve kohomoloji diyoruz. Örneğin; bu teoride Alexander ikiliğini ifade ederken yerel büzülebilirlik şartına ihtiyaç yoktur (Hatcher, 2002). Yine Aleksandrov-Čech homoloji terminolojisini kullanarak, Aleksandrov tarafından formulüze edilen Pontryagin ikiliğinin manifoldlar için karşılığını vereceğiz (Sklyarenko, 2011). Aşağıdaki ifade kimi kaynaklarda Aleksandrov-Pontryagin İkiliği olarak da bilinmektedir.

Teorem 3.3 (Pontryagin İkiliği, Pontryagin, 1955). \(G\) bir abel grup, \(M\) kompakt, bağlantılı, yönlendirilmiş bir \(n\)-manifold ve  \(A\), \(M\)'nin kompakt bir alt uzayı olsun. Eğer \(M\)'nin \(k\) dereceden ve \((k+1)\) dereceden Aleksandrov-Čech kohomoloji grubu tek elemanlı grup ise o zaman \(A\)'nın \(M\)'deki tümleyeninin indirgenmiş \(k\) dereceden homoloji grubuyla kendisinin \((n-k-1)\) dereceden kohomoloji grubu birbirine izomorfiktir. Yani \(\tilde{H}_k(M \setminus A ;G) \cong \tilde{H}^{n-k-1}(A;G)\).

Aleksandrov'un başka bir öğrencisi olan K.A. Sitnikov yukarıdaki ikilik teoreminin ifadesindeki \(A\)'nın üzerindeki kompaktlık koşulunu ortadan kaldırarak, herhangi bir alt uzay seçebileceğimizi kanıtlamıştır:

Teorem 3.4 (Sitnikov İkiliği, Sitnikov, 1951). \(G\) bir abel grup, \(M\) kompakt, bağlantılı, yönlendirilmiş bir \(n\)-manifold ve  \(A\), \(M\)'nin bir alt uzayı olsun. Eğer \(M\)'nin \(k\) dereceden ve \((k+1)\) dereceden Aleksandrov-\Čech kohomoloji grubu tek elemanlı grup ise o zaman \(A\)'nın \(M\)'deki tümleyeninin indirgenmiş \(k\) dereceden homoloji grubuyla kendisinin \((n-k-1)\) dereceden kohomoloji grubu birbirine izomorfiktir. Yani \(\tilde{H}_k(M \setminus A ;G) \cong \tilde{H}^{n-k-1}(A;G)\).

Şimdi Pontryagin İkiliği'nin, kompakt yerel topolojik gruplar ve onların karakterleri cinsinden ifade edilen orjinal versiyonu ele alacağız ve analize uygulamalarından bahsedeceğiz. Temel tanımlar ve teorem için, topolojik gruplar üzerine yazılan, Pontryagin'in dört ciltlik seçme çalışmalarından ikincisini takip edeceğiz (Pontryagin, 1986).

Üzerindeki topolojik uzay ve grup yapısı birbiriyle uyumlu olan nesnelere topolojik grup diyoruz. Matematiksel olarak ifade edecek olursak, bir topolojiye sahip \(G\) grubu için, şayet \(\alpha: G \times G \to G, \ \alpha(g,h)=g+h\) ve \(\beta: G \to G, \ \beta(g)= g^{-1}\) dönüşümleri sürekliyse \(G\) bir topolojik gruptur. \(G\) topolojik grubunun her noktası kompakt bir komşuluk tarafından içeriliyorsa ve üzerindeki grup işlemi değişmeliyse \(G\)'ye yerel kompakt değişmeli (YKD) topolojik grup diyoruz.

Çember üzerinde doğal bir grup yapısından bahsetmek mümkündür çünkü normları bir olan karmaşık sayılar çarpma işlemiyle birlikte bir grup oluşturur. Kümesel olarak ifade edecek olursak, \(\mathbb{T} = \{ z \in \mathbb{C} \ : \ |z|=1 \}\) ile verilen gruba çember grup denir. Şimdi bir YKD topolojik grup \(G\) verildiğinde, onun karakteri \(\chi\), grubun kendisinden çember grubuna bir sürekli grup homomorfizmasıdır yani her \(g,h \in G\) için \(\chi(gh) = \chi(g)\chi(h)\)'dir. \(G\)'nin üzerindeki tüm karakterlerin noktasal çarpma işlemiyle, yani \((\chi.\eta)(x)=\chi(x).\eta(x)\) ile bir YKD topolojik grup haline getirebiliriz. Bu yapıya \(G\)'nin ikilisi denir ve \(\widehat{G}\) ile gösterilir. Benzer bir şekilde \(\widehat{G}\)'nin ikilisini de tanımlayabiliriz, bunu da \(\widehat{\widehat{G}}\) ile gösterelim. Bu da bize bir YKD topolojik gruptan, onun ikilisinin ikilisi olan YKD topolojik gruba bir dönüşüm yazmamıza olanak sağlar: Verilen bir \(g \in G\) için, Pontryagin dönüşümünü \(\omega: G \to \widehat{\widehat{G}}, \ \omega_g(\chi) = \chi(g)\) kuralıyla tanımlayalım. Aşağıdaki gözlemimiz \(\omega\)'nın aynı zamanda bir grup homomorfizması olduğunu söyler: her \(\chi, \eta \in \widehat{G}\) için, grup işlemi korunur

Pontryagin İkiliği, Pontrayagin dönüşümünün aynı zamanda birebir ve örten bir dönüşüm yani bir grup izomorfizması olduğunu söyler. Dolayısıyla bir YKD topolojik grup ile onun ikilisinin ikilisi izomorfizma altında aynıdır:

Teorem 3.5 (Pontryagin İkiliği, 1934). \(G\) bir YKD topolojik grup ve \(\widehat{\widehat{G}}\) onun ikilisinin ikilisi olsun. O zaman Pontryagin dönüşümü \(\omega: G \to \widehat{\widehat{G}}\) bir grup izomorfizmasıdır yani \(G \cong \widehat{\widehat{G}}\).

Şimdi Pontryagin İkiliği'nin Fourier analizine önemli bir uygulamasından bahsedeceğiz. Fourier analizinin temel felsefesi, fonksiyonların, hali hazırda yapısını anladığımız trigonometrik fonksiyonların toplamlarıyla nasıl yaklaşılabileceğinin incelendiği alandır. Matematikten mühendisliğe, fizikten kimyaya ve biyolojiye uzanan çok geniş bir spektrumda Fourier analizinin uygulamalarından bahsetmek mümkündür.

Pontryagin İkiliği'nin doğal bir sonucu Fourier Tersinirlik Teoremi'nin genelleştirilmesi olacak. Bu teorem bize bir fonksiyonun şayet Fourier dönüşümünü biliyorsak, fonksiyonun kendisini belirlememizin mümkün olduğunu söyler (Rudin, 1962). Klasik Fourier analizini integraller vasıtasıyla, Lebesgue ölçüsüne göre yapıyoruz. Üzerinde integral alacağımız yapılar YKD topolojik gruplar olduğunda ise Lebesgue ölçüsü yerine Haar ölçüsüne ihtiyaç duyacağız.

Verilen bir \(X\) topolojik uzayı için, onun Borel kümelerinin koleksiyonu \(\mathcal{B}(X)\) tüm alt kümelerini ve bu alt kümelerin tümleyenlerini ve olası sayılabilir tüm kesişim ve birleşimlerini içerir. Şayet \(\mu: \mathcal{B}(X) \to [0,\infty]\) fonksiyonu aşağıdaki şartları sağlıyorsa bir Haar ölçüsü olarak adlandırılır:

(1) \(\mu(\emptyset) = 0\).
(2) Verilen bir sayılabilir, ikişer olarak ayrık Borel kümeleri ailesi \((E_i)_{i \in I}\) için \(\mu(\cup_{i \in I} E_i) = \sum_{i \in I} \mu(E_i)\).
(3) Her \(E \in \mathcal{B}(X)\) için \(\mu(E) = \inf \{\mu(U): E \subset U \ \text{ve} \ U, \ X\text{'de açık küme} \}\).
(4) Her \(x \in X\) ve herhangi bir \(E \in \mathcal{B}(X)\) için \(\mu(x+E) = \mu(X)\).

Verilen bir YKD topolojik grubu \(G\) için, Haar ölçüsü \(\mu\)'ye göre, \(G\) üzerindeki karmaşık değerli integrallenebilir tüm fonksiyonların uzayı \(L^1_\mu(G)\) aşağıdaki gibi tanımlanır:

$$L^1_\mu(G) = \Big \{ f: G \to \mathbb{C} \ \Big \vert \ \int_G |f(x)| d\mu(x) < \infty \Big \}.$$

Şimdi \(f \in L^1_\mu(G)\) olsun. O zaman \(f\)'nin \(\widehat{G}\) üzerindeki Fourier dönüşümü \(\widehat{f}\) aşağıdaki integral yardımıyla tarif edilir: $$\widehat{f}(x) = \int_G f(x) \overline{\chi(x)} d\mu(x).$$

Artık Pontryagin İkiliği de içerisinde doğrudan gözükecek biçimde Fourier Tersinirlik Teoremi'nin ifadesini yazacak kavram setine sahipiz. [10]

Teorem 3.6 (Fourier Tersinirlik Teoremi). \(G\) bir YKD topolojik grup ve \(\mu\), \(G\) üzerinde bir Haar ölçüsü olsun. O zaman \(\widehat{G}\) üzerinde biricik \(\widehat{\mu}\) Haar ölçüsü vardır öyle ki verilen her \(f \in L^1_\mu(G)\) için \(\widehat{f} \in L^1_{\widehat{\mu}}(\widehat{G})\)'dir ve

$$f(x) = \int_{\widehat{G}} \widehat{f}(x) \chi(x) d\widehat{\mu}(x).$$ Baska bir deyişle aşağıdaki eşitliği elde ederiz:

$$f(x) = \widehat{\widehat{f}}(\omega_{x^{-1}}).$$

GEOMETRİK TOPOLOJİ

Günümüz fizik biliminin yapı taşı olan uzay-zamanı \(4\)-manifoldlar ile modelliyoruz. Dolayısıyla bu yapıları matematiksel olarak kavrama ve sınıflandırma uğraşı, dünyayı ve evreni anlama arayışımızla ayrılmaz bir bütündür. Klasik fizik teorilerini modellemek için bile türev kavramına ihtiyaç duyuyoruz. Örneğin, konum fonksiyonun zamana göreve türevi hız fonksiyonunu, hız fonksiyonunun yine zamana göre türevi ise ivme fonksiyonun verir. Şimdi türev kavramını \(4\)-manifoldlara [11] asıl taşıyacağımızı tartışacağız, bu yüzden şu ana kadar manifold dediğimiz yapıları yeni kavramdan farklılaştırmak adına hali hazırda kullandığımız yapıları topolojik manifold olarak adlandıralım. Bir topolojik manifold üzerindeki türev olgusunu tarif ettiğimiz yapıya da pürüzsüz yapı diyelim. Herhangi bir topolojik manifold üzerinde pürüzsüz yapının ne olduğunu tanımlamadan önce akla gelebilecek iki temel soru var. İlk olarak bu yapılar her zaman var mıdır? Şayet varlarsa biricik midir? Bu iki sorunun cevabı da \(4\)-manifoldlar için çoğu zaman hayır olacak. Pürüzsüz yapıya sahip topolojik \(4\)-manifoldlara pürüzsüz \(4\)-manifold diyeceğiz. Birden fazla pürüzsüz yapı ihtiva eden nesneler de egzotik \(4\)-manifold olarak adlandırılır. Bir kıyaslama yapmak adına, örneğin, \(n=4\) değilse \(\mathbb{R}^n\) üzerinde tek bir pürüzsüz yapı vardır (Stallings, 1962). Buna karşın \(\mathbb{R}^4\) üzerine sayılamaz çoklukta pürüzsüz yapı konulabilir dolayısıyla bir egzotik \(4\)-manifoldtur (Taubes, 1987).

Bir \(X\) topolojik \(4\)-manifoldu üzerindeki bir pürüzsüz yapı, birbirine denk atlasların bir koleksiyonudur. \(X\) için bir atlas, pürüzsüz geçiş dönüşümleri \(\varphi_{\alpha\beta}\) ile birlikte \(4\)-manifoldu \(X\)'ı kaplayan \((U_\alpha,\varphi_\alpha)\) koordinat çizelgelerinin bir sistemidir. Şayet iki atlasın birleşimleri yine bir atlas ise, birbirlerine denktir diyoruz. Şayet iki pürüzsüz \(4\)-manifold arasında pürüzsüz yapıyı koruyan, yani kendisi ve tersi pürüzsüz olan, bir homeomofizma varsa ona diffeomorfizma diyoruz.

Bir \(G\) grubunun sonlu bir temsili verildiğinde, \(\pi_1(X) = G\) temel grubuna sahip aşağıdaki gibi bir pürüzsüz kapalı \(4\)-manifold \(X\)'i inşa edebiliriz: Üreteç başına bir tane karşılık getirecek şekilde \(S^1 \times S^3\)'lerin bağlantılı toplamını alırız ve \(S^1 \times B^3\)'leri \(S^2 \times B^2\) ile değiştirecek şekilde ilişkilere karşılık gelen ilmekler üzerinde ameliyat yaparız.

Sovyet matematikçi S.I. Adyan göstermiştir ki sonlu grup temsillerinin tek elemanlı gruba karşılık gelip gelmediklerini belirlemek için uygulanabilecek hiçbir algoritma yoktur (Adyan, 1955). Yine bir diğer Sovyet matematikçi A. A. Markov [11] bu sonucu kullanarak aşağıdaki teoremi kanıtlamıştır.

Teorem 4.1 (Markov, 1958). Herhangi iki kapalı \(4\)-manifoldun birbirlerine diffeomorfik olup olmadığını belirleyebilecek bir algoritma yoktur.

Markov'un bu sonucundan sonra topolojiciler en azından temel grubu tek elemanlı grup olan bağlantılı \(4\)-manifoldları sınıflandırabilir miyiz sorusuna odaklanmışlardır. Bu tip \(4\)-manifoldlara basit bağlantılı diyoruz. Şayet Hurewicz teoremini, Poincar'e İkiliği'ni ve evrensel katsayılar teoremini kullanırsak \(4\)-manifoldun homoloji gruplarına dair hızlıca aşağıdaki gözlemi yapabiliriz:

$$H_0(X)=H_4(X) = \mathbb{Z}; \ H_1(X)=H_3(X) = 0; \ H_2(X)= \mathbb{Z}^r, r \geq 0.$$

Dahası \(4\)-manifoldun ikinci homolojisi üzerinde, her zaman bir simetrik, unimodüler ve iki-doğrusal kesişim formu vardır:

$$Q_X: \mathbb{Z}^r \times \mathbb{Z}^r \to \mathbb{Z}.$$

Şimdi bu formda her elemanı kendisiyle işleme soktuğumuzda bize bir çift tamsayı veriyorsa forma çift, aksi durumda ise tek diyoruz.

Saydığımız özelliklere sahip herhangi bir kesişim formunu gerçel sayılar \(\mathbb{R}\) üzerinde \(Q_X = m\langle1\rangle+n\langle-1\rangle\) şeklinde ayrıştırabiliriz, üstelik bizim durumumuzda bu sayılar \(4\)-manifoldun pozitif ve negatif özvektörlerinin sayısını tarif eder ve toplamları ikinci Betti sayısını \(b_2\) verir: \(m= b_2^+(X)\), \(n= b_2^-(X)\) ve \(b_2 = b_2^+ + b_2^-\). Bu iki sayı arasındaki fark ise \(4\)-manifoldların işaret denilen ve \(\sigma\) ile gösterilen önemli bir değişmezini oluşturur:

$$\sigma(X) = b_2^+(X) - b_2^-(X).$$

Bu değişmezle birlikte \(4\)-manifoldların kesişim formları üzerindeki ilk büyük sonuç, Sovyet matematikçi V.I. Rokhlin'in aşağıdaki ünlü teoremidir:

Teorem 4.2 (Rokhlin, 1952). \(X\) bir pürüzsüz, kapalı, basit bağlantılı \(4\)-manifold olsun. Eğer \(Q_X\) çift ise \(\sigma(X)\), \(16\)'ya tam bölünür.

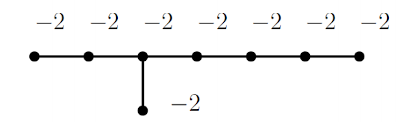
Bir kesişim formunda her sıfırdan farklı elemanın aldığı değerin işareti aynıysa forma belirli diyoruz. Rohklin'den sonra \(4\)-boyutlu manifoldların topolojisine dair en kapsamlı gelişmeye İngiliz matematikçi S.K. Donaldson imza atmıştır. Bu çalışmasıyla birlikte fizik ile matematik bilimleri arasındaki derin ilişki bir kez daha gün yüzüne çıkmıştır. Makalesinin başlığında da nitelediği gibi, Donaldson ayar teorisini kullanarak \(4\)-manifoldların topolojisine dair derin bir sonuç ortaya koymuştur. İnstantonları merkeze alan yaklaşımı, kökeni kuantum alan teorisine dayanan Yang-Mills ayar teorisini modelleyen kısmi diferansiyel denklemlerinin özel bir çözümüne dayanmaktadır (Donaldson, 1983). Donaldson bu sonucu neticesinde, 1986 yılında düzenlenen Uluslararası Matematik Kongresi'nde, matematiğe bu katkısından dolayı Fields Madalyası'yla ödüllendirilmiştir.

Teorem 4.3 (Donaldson, 1983). \(X\) bir pürüzsüz, kapalı, basit bağlantılı \(4\)-manifold olsun. Eğer \(Q_X\) belirli ise köşegenleştirebilirdir, yani bazı \(n \in \mathbb{Z}\) için \(Q_X \cong n\langle1\rangle\).

M. Freedman kapalı, basit bağlantılı topolojik \(4\)-manifoldları sınıflandırmıştır (Freedman, 1982). Bunun neticesinde dördüncü boyutta Poincar'e sanısını da içeren bir çok önemli sonucu kanıtlamıştır. Freedman bu sarsıcı sonuçları neticesinde, Donaldson ile aynı yıl Fields Madalyası'na layık görülmüştür. Donaldson'ın sonuçlarıyla Freedman'ın sonuçları arasındaki kontrast, \(4\)-manifoldların üzerindeki topolojik ve pürüzsüz yapı arasındaki kapatılamaz uçurumu daha berrak hale getirmiştir. Freedman'ın bu meşhur sonuçlarını elde ettiği makalesinden kesişim formlarıyla ilgili şu teoremi alıntılıyalım.

Teorem 4.4 (Freedman, 1982). Her simetrik, ünimodüler, iki-doğrusal ve çift kesişim formu \(Q\) için, homeomorfizma altında biricik kapalı, basit bağlantılı, topolojik \(4\)-manifold \(X\) vardır öyle ki \(Q_X \cong Q\).

Freedman'ın teoremini kullanarak \(E_8\) Dynkin diyagramına karşılık gelen kesişim formuma sahip bir topolojik \(4\)-manifoldtan bahsedebiliriz, \(W\) diyelim. Gösterilebilir ki \(W\)'nun kesişim matrisi aşağıdaki gibidir ve dolayısıyla \(\sigma(W) = -8\)'tir. Bu durumda Rokhlin'in teoremi bize bu \(4\)-manifoldun üzerine pürüzsüz yapı konulamayacağını söyler.[13]

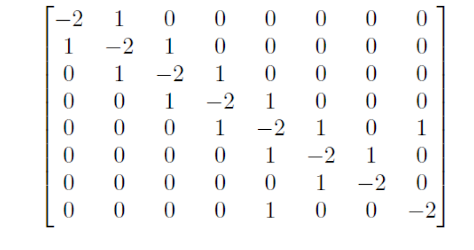
Sonuç 4.5 Pürüzsüz olmayan topolojik $4$-manifoldlar vardır.

Amerikalı matematikçi E.E. Moise göstermiştir ki her topolojik \(3\)-manifold biricik şekilde pürüzsüzleştirebilir, yani üçüncü boyutta topolojik manifoldların kategorisiyle pürüzsüz manifoldların kategorisi eştir (Moise, 1952). Ancak gördüğümüz gibi dördüncü boyutta pürüzleştirilemeyen topolojik \(4\)-manifoldlar var. Bu derin fark topolojicileri iki boyut arasındaki ilişkiyi çalıştırmaya da itmiştir. Bunun hemen arifesindeki en derin sonuçlardan biri yine Rokhlin tarafından elde edilmiştir.

Teorem 4.6 (Rokhlin, 1951). Her kapalı, yönlendirilmiş \(3\)-manifold bir kompakt, yönlendirilmiş, pürüzsüz \(4\)-manifoldu sınırlar.

Şimdi \(Y_0\) ve \(Y_1\) iki kapalı, yönlendirilmiş \(3\)-manifold olsun. Kenarı \(-(Y_0) \cup Y_1\) olan kompakt, yönlendirilmiş, pürüzsüz \(4\)-manifoldlara kobordizm diyoruz. Bu ilişki vasıtasıyla bu tür \(3\)-manifoldların kümesi üzerinde bir denklik bağıntısı inşa edebiliriz. Bu sayede, manifoldlar arasındaki bağlantılı toplam işlemiyle birlikte bir grup yapısından bahsetmek mümkün hale gelir. Bu gruba kobordizm grubu diyoruz ve \(\Omega_3\) ile gösteriyoruz. Rokhlin'in yukarıdaki teoreminin doğrudan bir sonucu bu grubun tek elemanlı grup olduğudur.

Sonuç 4.7. Kobordizm grubu tek elemanlı gruptur, yani \(\Omega_3 = {0}\).

Fransız matematikçi Poincaré ünlü sanısının ilk versiyonuna karşıt örnek vermiştir ve problemi revize etmiştir. Bu \(3\)-manifolda bugün Poincaré homoloji küresi diyoruz. Bu tanımdaki homoloji küresi vurgusu manifodumuzun homoloji gruplarının \(S^3\)'ün homoloji gruplarıyla aynı olduğu manasına gelmektedir.

Şimdi \(E_8\) diyagramını yeniden düşünecek olursak buradan başlayarak bir pürüzsüz \(4\)-manifold inşasından bahsedebiliriz. \(E_8\)'in her köşesine karşılık \(S^2\) üzerinde, orada yazan tam sayıya karşılık gelen Euler sayısına sahip bir \(D^2\) demetini ele alalım. Şayet iki köşe arasında bir kenar varsa bu iki disk demetini tesisatlayabiliriz. Bu işlem köşe sayısına bağlı olarak sonlu bir işlemdir ve neticesinde kompakt, basit bağlantılı, yönlendirilmiş, pürüzsüz bir \(4\)-manifold ederiz. Bu tip manifoldlara tesisat \(4\)-manifold diyoruz. Poincar'e homoloji küresi de tam olarak \(E_8\)'e karşılık gelen bu tip \(4\)-manifoldun kenarıdır (Saveliev, 2002).

Örneğin bu manifoldun temel grubu tek elemanlı grup olmadığı için \(S^3\)'e homeomorfik olmadığını biliyoruz. Bu tip manifoldları çalışmak için yine kobordizm ilişkisinin bir varyasyonuna ihtiyaç duyacağız. Ancak bunu yazmadan önce iki önemli ve kısıtlayıcı sonucumuz var. İlki Rokhlin'in teoremi. Şayet homoloji kürelerinin kümesi üzerinde \(4\)-manifolda hiçbir koşul koymazsak yine bir tek elemanlı grup meydana gelecek. Diğer yandan Freedman'ın sınıflandırmasının sonucu gereği biliyoruz ki her homoloji küresi bir büzülebilir topolojik \(4\)-manifoldu sınırlıyor. O yüzden aşağıdaki hassas tanıma ihtiyacımız var.

Şu andan itibaren \(Y_0\) ve \(Y_1\) iki yönlendirilmiş homoloji küresi olsun. Bu sefer ise kenarı \(-(Y_0) \cup Y_1\) olan ve \(S^3 \times [0,1]\)'in homolojisine sahip, kompakt, yönlendirilmiş, pürüzsüz \(4\)-manifoldlara homoloji kobordizm diyoruz. Bu ilişki ile benzer bir şekilde homoloji kürelerinin kümesi üzerine bir grup yapısı oluşturuyoruz. Ortaya çıkan yapıyı homoloji kobordizm grubu olarak adlandırıyoruz ve \(\Theta_{\mathbb{Z}}^3\) ile gösteriyoruz.

Rokhlin'in bir diğer önemli sonucu da bu gruptan iki elemanlı grup \(\mathbb{Z} / 2\mathbb{Z}\)'e yazılabilen bir örten grup homomorfizmasını varlığıdır ve yaygın bir biçimde Rokhlin değişmezi veya Rokhlin homomorfizması olarak bilinir.

Teorem 4.8 (Rokhlin, 1952). \(Y\) bir homoji küresi, \(W\) kenarı \(Y\) olan bir kompakt, yönlendirilmiş, pürüzsüz \(4\)-manifold olsun. O zaman

$$\mu: \Theta_{\mathbb{Z}}^3 \to \mathbb{Z} / 2\mathbb{Z}, \ \ \mu(Y) = \sigma(W)/8 \mod 2$$

bir örten grup homomorfizmasıdır.

Poincaré homoloji küresi, \(E_8\)'e karşılık gelen tesisat \(4\)-manifoldun kenarı olduğundan Rokhlin değişmezi \(1\)'dir. Dolayısıyla aşağıdaki sonucu elde ederiz.

Sonuç 4.9. Homoloji kobordizm grubu tek elemanlı grup değildir, yani \(\Theta_{\mathbb{Z}}^3 \neq { 0 }\).

Rokhlin değişmezi ve homoloji kobordizm grubu modern topolojinin en temel ve merkezi nesnelerinden olagelmişlerdir (Manolescu, 2018). Örneğin, Manolesu'nun inşa ettiği \(\beta\) değişmezi hem Rokhlin'in \(\mu\) değişmezinin tamsayılara genellemesidir hem de aynı zamanda \(\Theta_{\mathbb{Z}}^3\) grubunun değişmezidir. Bu değişmezin varlığı sayesinde Manolescu meşhur Üçgenleştirme Sanısı'nı çürütmüştür. Bu sayede boyutu \(5\)'ten büyük eşit topolojik manifoldların her zaman üçgenleşleştirilemeyeceğini biliyoruz (Manolescu, 2016). Casson'un çalışmaları sayesinde dördüncü boyutta da üçgenleştirme sanısının doğru olmadığını biliyoruz (Akbulut-McCarthy, 1990). Üç ve üçten küçük boyutlarda ise sanının doğruluğu kanıtlanmıştır.

SONUÇ

Sovyet topolojisinin kırk bir yıllık tarihini matematiğiyle birlikte sunan bu çerçeve yazısı bu mecraya giriş niteliğinde kabul edilmelidir. Bir kaç kez vurgulandığı üzere bu makale üretilen matematiksel bilginin tümüne değil üç temel topoloji alanındaki kimi mihenk taşlarına odaklanmıştır. Çeşitlendirmeye ve derinleştirmeye tarihinin kendisinin izin verdiği üzere açıktır.

Yazım sürecinde, mevcut matematiksel bilgiyi açıklamak kadar güncel matematik ile bağını tarif etmek de eş düzeyde önemsenmiştir. Bu nedenle matematiksel tanımlar, ifadeler ve teoremler yer yer çok teknikleşmiş olup, bunun dozunun biraz daha azaltılması Sovyet topolojisinin kendisini yadsıyacağı ve nitelikli üretimin hissedilmemesine sebebiyet vereceği için özellikle kaçınılmıştır. Bununla birlikte teorilerin kavranabilmesi için mümkün olan en sade ve anlaşılır örnekler ve anektodlar seçilmeye çalışılmıştır. Bu uğurda özellikle matematiksel tanımların arkasındaki sezginin açıklanmasına gayret gösterilmiştir.

İnsanlık olarak gördüğümüzü kavrama ve değiştirme maceramızdaki en büyük araçlardan biri olagelen topolojinin matematik, fizik, kimya ve biyoloji bilimleri olan sıkı ilişkisi kuşkusuz ki derinleşerek devam edecektir. Makalenin bir kısmını sunduğu üzere bu kavrayışımızı Sovyet bilim insanlarına da borçluyuz.

KAYNAKLAR

Akbulut, S., McCarthy, J. D. (1990). Casson's Invariant for Oriented Homology Three-Spheres: An Exposition.(MN-36) (Vol. 36). Princeton University Press.

Adyan, S.I. (1955). Algorithmic unsolvability of problems of recognition of certain properties of groups. Doklady Akad. Nauk SSSR (N.S.), 103. 533–535.

Aleksandrov, A.D. (1947). Geometry and topology in the Soviet Union. I. Uspekhi Matematicheskikh Nauk, 2(4). 3-58.

Alexandroff, P.S. (1924). Über die Metrisation der im Kleinen kompakten topologischen Räume. Mathematische Annalen, 92(3). 294-301.

Alexandrov, P.S., Urysohn, P.S. (1929). Mémoire sur les espaces topologiques compacts. Koninklijke Nederlandse Akademie van Wetenschappen Te Amsterdam, Proceedings of the Section of Mathematical Sciences, 14.

Alexander, J.W. (1915). A proof of the invariance of certain constants of analysis situs. Transactions of the American Mathematical Society, 16(2). 148-154.

Boi, L. (2019). The role of intuition and formal thinking in Kant, Riemann, Husserl, Poincar'e, Weyl, and in current mathematics and physics. Kairos, 22(1).

Deitmar, A., Echterhoff, S. (2014). Principles of harmonic analysis. Springer.

Donaldson, S. K. (1983). An application of gauge theory to four-dimensional topology. Journal of Differential Geometry, 18(2), 279-315.

Euler, L. (n.d.). (1970-1979). The Great Soviet Encyclopedia, 3rd Edition. Erişim tarihi: 16.08.2021 https://encyclopedia2.thefreedictionary.com/Euler%2C+Leonhard

Euler, L. (1741). Solutio problematis ad geometriam situs pertinentis. Commentarii academiae scientiarum Petropolitanae, 128-140.

Euler, L. (1758). Elementa doctrinae solidorum, Novi Commentarii Academiae Acientiarum Petropolitanae 4 (1752/3), p. 109-140. reprinted in Opera Omnia, Series I, Vol. 26. 71-93.

Hatcher, A. (2002). Algebraic Topology. Cambridge University Press, Cambridge. xii+544.

Freedman, M.H. (1982). The topology of four-dimensional manifolds. Journal of Differential Geometry, 17 (3). 357-453.

Kline, M. (1990). Mathematical Thought from Ancient to Modern Times: Volume 3. Oxford University Press.

Lapko, A.F., Lyusternik, L.A. (1957). Mathematical sessions and conferences in the USSR. Uspekhi Matematicheskikh Nauk, 12(6). 47-130.

Mathematics (n.d.). (1970-1979). The Great Soviet Encyclopedia, 3rd Edition. Erişim tarihi: 16.08.2021 https://encyclopedia2.thefreedictionary.com/mathematics

Moise, E. (1952). Affine structures in \(3\)-manifolds. V. The triangulation theorem and Hauptvermutung. Annals of Mathematics, 56. 96-114.

Manolescu, C. (2016). Pin(2)-equivariant Seiberg-Witten Floer homology and the triangulation conjecture. Journal of the American Mathematical Society, 29 (1) 147-176.

Manolescu, C. (2018). Homology cobordism and triangulations. Proceedings of the International Congress of Mathematicians: Rio de Janeiro 2018.

Markov, A. (1958). The insolubility of the problem of homeomorphy. Doklady Akad. Nauk SSSR (N.S.), 121. 218–220.

Poincaré, H. (1895). Analysis situs. Paris, France: Gauthier-Villars. 1-121

Pontrjagin, L.S. (1934). The theory of topological commutative groups. Annals of Mathematics. 361-388.

Pontryagin, L.S. (1986). Selected Works, vol. 2. Topological Groups. Ed. R.V Gamkrelidze. Trans. A. Brown. 3rd ed. Classics of Soviet Mathematics. New York: Gordon & Breach Science Publishers.

Raman-Sundström, M. (2015). A pedagogical history of compactness. The American Mathematical Monthly, 122(7). 619-635.

Rokhlin, V.A. (1951). A three-dimensional manifold is the boundary of a four-dimensional one. Doklady Akad. Nauk SSSR (N.S.), 81. 355 - 357.

Rokhlin, V.A. (1952). New results in the theory of four-dimensional manifolds. Doklady Akad. Nauk SSSR (N.S.), 84. 221 - 224.

Sitnikov, K. (1951). The duality law for non-closed sets. Doklady Akad. Nauk SSSR (N.S.), 81. 359-362.

Sklyarenko, E.G. (2011). Pontryagin duality. Encyclopedia of Mathematics. Erişim tarihi: 16.08.2021 http://encyclopediaofmath.org/index.php?title=Pontryagin_duality&oldid=49720

Riemann, B. (1851). Grundlagen fur eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. Adalbert Rente.

Rudin, W. (2017). Fourier analysis on groups. Courier Dover Publications.

Saveliev, N. (2002). Invariants of Homology 3-spheres (Vol. 140). Springer Science & Business Media.

Stallings, J. (1962). The piecewise-linear structure of Euclidean space. Mathematical Proceedings of the Cambridge Philosophical Society, 58(3). 481-488.

Şavk, O. (2019a). Königsberg’in yedi köprüsü ve topolojinin doğuşu. Bilim ve Aydınlanma Akademisi. Erişim tarihi: 16.08.2021 https://bilimveaydinlanma.org/konigsbergin-yedi-koprusu-ve-topolojinin-dogusu/

Şavk, O. (2019b). Euler’in çokyüzlü formülü. Bilim ve Aydınlanma Akademisi. Erişim tarihi: 16.08.2021 https://bilimveaydinlanma.org/eulerin-cokyuzlu-formulu/

Şavk, O. (2019c). Euler’in çokyüzlü formülünün kanıtı. Bilim ve Aydınlanma Akademisi. Erişim tarihi: 16.08.2021 https://bilimveaydinlanma.org/eulerin-cokyuzlu-formulunun-kaniti/

Taubes, C. H. (1987). Gauge theory on asymptotically periodic 4-manifolds. Journal of Differential Geometry, 25(3). 363-430.

Whitney, H. (1992). Moscow 1935: topology moving toward America. In Hassler Whitney Collected Papers (pp. 1-21). Birkhäuser Boston.

[1] Bu formülün Descartes tarafından daha önce ifade edildiği biliniyor. Ayrıntılar için (Şavk, 2019c) yazısına göz atılabilir.

[2] Topolojik eşleme kavramının tanımını bir sonraki bölümde vereceğiz ve bu tip dönüşümleri homeomorfizma olarak adlandıracağız.

[3] Not düşmek gerekir ki Uryson 1924'te, henüz 26 yaşındayken, Britanya'da yüzerken hayatını kaybetmiştir.

[4] Çoğu zaman böylesine uzun isim listelerinin makale içinde yer alması okuyucuyu dağıtacağını düşünüyorum. Ancak bu istisna özellikle matematik tarihine ve topolojiye meraklı bir okuyucuyu yazıya daha fazla odaklayacağı inancıyla yapıldı.

[5] Neredeyse tüm genel topoloji alanını sıfırdan anlatmaya denk düşeceği için olanaksız bir uğraştır.

[6] Kompakt kavramının analizden başlayarak topolojiye uzanan tarihsel serüveni için Raman-Sundström (2015) makalesine başvurulabilir.

[7] Örneğin, bir noktada kendini kesmesine veya bir sivri çıkıntıya sahip olmasına izin vermiyoruz.

[8] Mannigfaltigkeit kavramına daha öncesinde Immanuel Kant’ın Saf Aklın Eleştirisi adlı eserinde rastlamak mümkün. Ancak Riemann’ın Kant’tan esinlenerek bu kelimeyi türettiğine dair somut bir veri bulunmuyor (Boi, 2019).

[9] Örneğin, \(\mathbb{R}^2\)'deki tarak uzayı büzülebilir ancak yerel büzülebilir değildir. Bu tanımla, topolojik uzaylarda meydana gelebilecek yerel patolojilerin önüne geçiyoruz.

[10] Bu yönde çok daha derinlemesine bilgi edinmek için okuyucu Rudin (2017) ve Deitmar ve Echternoff (2014) kitaplarına göz atabilir. Gösterimler çok daha modern olduğu için, teoremlerin ifadelerinde bu kaynaklara da başvurulmuştur.

[11] Bu genelleme herhangi bir boyuttaki manifold için de aynıdır.

[12] Markov'un babası da A.A. Markov ismine sahip bir matematikçi olduğu için kimi kaynaklarda kendisinen A.A. Markov jr. olarak bahsedilmektedir.

[13] Donaldson'ın teoremi sadece \(W\)'nun değil aynı zamanda \(W\)'nun kendisiyle bağlantılı toplamı olan \(W\) # \(W\) 'nun üzerine de pürüzsüz yapı konulamayacağını söyler