Matematiğin mitleri: Altın oran

Altın oranın birçok şaşırtıcı özelliği var. Ama bu gerçekten doğanın bir sırrı ve güzelliğin timsali midir?

[BAA - Matematik/ Çeviri: Oğuz Şavk]

Çoğunuz altın oran denilen sayıyı duymuşsunuzdur. Örneğin, kitap/film olan da Vinci Kodu'nda ve matematiğin gerçek dünyada nasıl önemli olduğunu göstermeyi amaçlayan birçok makale, kitap ve okul projesinde yer almaktadır. Birçok yazar tarafından (da Vinci Kodunun yazarı da dahil olmak üzere), doğadaki tüm güzel desenlerin temeli olarak tanımlanmıştır ve bazen de kutsal oran olarak adlandırılmaktadır. Sanatın ve mimarinin çoğunun altın oranın verdiği oranlarda özellikler içerdiği iddia edilmektedir. Örneğin, hem Parthenon'un hem de piramitlerin bu oranda olduğu iddia edilmektedir. Altın oranın insan vücudunda, örneğin bir yetişkinin boyunun göbek deliğinin yüksekliğine veya ön kol uzunluğunun elin boyuna oranı olarak ortaya çıktığı da iddia edilmiştir.

Oysa matematiği gerçek dünyaya uyguladığım kariyerim boyunca, altın orana tam olarak iki kez rastladım. Evet iki kez! Dolayısıyla altın oran için yapılan bu büyük iddialardan herhangi biri doğru mudur?

Yeniden altın oran nedir?

Altın oranın gerçekte ne olduğunu hızlı bir şekilde hatırlatarak başlayalım. Antik Yunan matematikçi Öklid tarafından aşağıdaki gibi tanımlanmıştır. İki parçaya bölmek istediğiniz bir doğru parçamız olduğunu düşünün. Bunu, tüm parça ile iki parçanın daha uzun arasındaki oran, iki parçanın daha uzun ve daha kısa olanı arasındaki oranla aynı olacak şekilde bölmek istersiniz. Bu oran ne olmalı?

Biraz matematik bu oranın

\( \phi = \frac{1 + \sqrt{5}}{2} \approx 1.618. \)

olacağını ortaya çıkarır. ϕ'nin iki uzunluk arasında bir oran olarak tanımlanmış olması, ister bir yüz ister bir bina olsun, içinde doğru parçaları olan bir şeye baktığınızda onu arayabileceğiniz anlamına gelir.

İnsan vücudundaki altın oran

Altın oranın insan vücudundaki oranların çoğunun merkezinde olması gerekiyordu. Bunlar, kusursuz yüzün şeklini ve ayrıca göbek deliği yüksekliğinin vücut yüksekliğine oranını içerir. Gerçekten de kusursuz insan yüzünün hemen hemen her oranının altın oranla bir bağlantısı olduğu iddia edilmektedir.

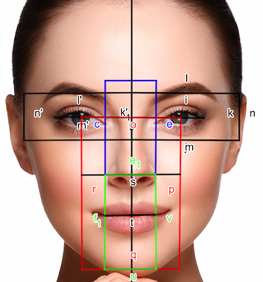
Ancak, bunların hiçbiri doğru değil, uzaktan bile alakası yok. Vücudun birçoğu 1 ile 2 arasında bir yerde bulunan birçok olası orana sahiptir. Eğer yeterince üstüne düşünürseniz, altın oranın değerine yakın sayılar elde etmeye mahkûm olursunuz (yaklaşık 1.618). Bu özellikle ölçtüğünüz şeyler özellikle iyi tanımlı değilse (yukarıdaki resimde olduğu gibi) doğrudur ve tanımı bulmak istediğiniz oranları elde edecek şekilde değiştirmek mümkündür.

Yeterince kendinizi zorlarsanız, insan vücudunda 1.6, 5/3, 3/2'ye ve 2, 42/26'nın kareköküne yakın oranlar bulacaksınız. Gerçekten de 1 ve 2 arasındaki çoğu sayı vücudun iki kısmının yaklaşık oranına denk gelecektir. Güneş sisteminde de benzer yapay desenler gözlenir (ayrıca aralarından seçim yapabileceğiniz birçok farklı orana sahiptir). Altın oran bir irrasyonel bir sayı olduğu için, bunu hiçbir ölçümde tam olarak göremeyeceğinizi de unutmayın.

Bütün bunlar insan beyninin yanıltıcı ilişkiler bulma yolunun bir örneğidir. Gerçekten de yeterli veri verildiğinde, hemen hemen her hipotezle uyumlu kalıplar bulmak mümkündür. Bunu görmenin iyi bir yolu, güzel güneşli bir günde dışarı çıkıp bulutlara bakmaktır. Er ya da geç yeni bir kalıba uyan bir bulut bulacaksınız.

Bu fenomen, bir noktayı kanıtlamak için verilerde yanıltıcı ilişkiler bulunduğunda aslında oldukça tehlikeli olabilir. Örneğin, yanlış suçlamalara ve hatta yanlış kanılara yol açabilirler.

Spiraller, altın ve diğerleri

\( A / B \)'nin altın oran olacak şekilde bir doğruyu \(A \) ve \(B \) doğru parçalarına bölerseniz ve ardından \(A+B \) ve \(A \) kenarlarıyla bir dikdörtgen oluşturursanız, o zaman bu dikdörtgen bir altın dikdörtgen olarak adlandırılır.

Yeni oluşturduğumuz altın dikdörtgen, bir kare ve daha küçük bir dikdörtgenden oluşuyor ki bunun kendisi bir altın bir dikdörtgen. Bu altın dikdörtgen yine bir kare ve kendisi de altın bir dikdörtgen olan daha küçük bir dikdörtgenden oluşur. Ve benzeri şekilde devam eder.

Daha ve daha küçük altın dikdörtgenler dizisini kullanarak, sarmala benzer bir şekil oluştururuz. Basitçe altın dikdörtgenlerde görünen karelerin her birine bir çeyrek çember çiziniz.

Genellikle bu sarmal benzeri şeklin doğa ve sanatın birçok yerinde bulunabileceği iddia edilmektedir. Örneğin, bir nautilus kabuğunun şekli, bir galaksinin şekli, bir kasırganın şekli ve hatta bir dalganın şekli olarak.

Burada iki problem var. İlk olarak, şekil sarmal değildir. Dairesel yayların bir dizisidir. Bir yaydan diğerine geçerken sarmalın eğriliği sıçrar. Herhangi bir doğal fenomende bu tür sıçramaları görmemiz pek olası değildir. Aslında, şekil sadece gerçek bir sarmala bir yaklaşımdır.

Yaklaştığı sarmal şekil bir logaritmik sarmal örneğidir. Bu tür sarmallar doğada çok yaygındır. e'nin doğal logaritmanın tabanı olduğu kutupsal denkleme sahiptirler.

\( r=a^{b \theta}, \)

Doğada, bu tür sarmalları her yerde, bağlama bağlı olacak şekilde a ve b'nin farklı değerleriyle görüyoruz. Bu sarmalların bu kadar yaygın olmasının nedeni, öz-benzerlik özelliğine sahip olmalarıdır. Bu, sarmalı sabit bir açıyla döndürürseniz, orijinalin yeniden ölçeklenmesi olan bir sarmal elde edeceğiniz anlamına gelir. Bu sözde altın sarmal belirli bir b değerine sahiptir

\( b= \frac{\mathrm{ln} \phi }{(\pi / 2)} = 0.3063489... \)

Burada ϕ altın orandır (ve dereceler radyan cinsinden ölçülür).

Bu sayının herhangi bir şekilde özel olmasının hiçbir nedeni yoktur. Nautilus kabuğu logaritmik bir sarmaldır çünkü öz-benzerlik özelliği, kabuğun şekil değiştirmeden büyümesine izin verir. Nautilus kabuğu için gözlenen b değerleri yukarıdaki değerle bir ilişki göstermez, gerçek kabuklarda en yaygın biçimde b = 0.18 değeri görülür.

Sanat ve mimari

Burada dikkatli olmak zorundayız. Le Corbusier (Modulor sisteminde) gibi bazı sanatçıların sanat eserlerinde altın oranı kasten kullandıkları kesinlikle doğrudur. Çünkü altın dikdörtgenin oranlarının insan gözüne özellikle hoş geldiği ve estetik olarak altın dikdörtgeni diğer tüm dikdörtgenlere tercih ettiğimiz iddia edilmektedir. Bu yüzden onları sanat eserlerinde kullanmak mantıklıdır. Daha sonra altın oranın hemen hemen tüm diğer sanat ve mimari eserlerinde görülebileceği iddia edilmektedir.

Altın dikdörtgenin özellikle hoş olduğuna dair kanıtlar oldukça zayıftır. İnsan gruplarına farklı dikdörtgenler gösteren psikolojik çalışmalar, ikinin karekökünün bire oranının diğerlerine göre sıklıkla tercih edilmesi ile birlikte geniş bir yelpazede tercihlerin olduğunu gösteriyor. Hangisini tercih ettiğinizi görmek için aşağıdaki dikdörtgenler üzerinde kendinizi test ediniz.

Keith Devlin'in Devlin'in Açısı: Kaybolmayacak Mit'e göre, altın oranın estetikle herhangi bir ilişkisi olduğu fikri esasen biri yanlış aktarılma ve diğeri yaratıcılığa sebep olmak üzere iki tip insandan geliyor. Yanlış aktarılan yazar 1509'da De Divina Proportione adlı bir kitabı yazan Luca Pacioli'ydi. Kitap altın orandan sonra adlandırıldı, ancak altın orana dayanan bir estetik teorisi ya da sanat ve mimariye uygulanması gerektiğini iddia etmedi. Böyle bir görüş 1799'da Pacioli'ye hatalı olarak atfedildi.

Pacioli, Leonardo da Vinci ile yakın arkadaştı ve sık sık Leonardo'nun kendisinin de resimlerinde altın oranı kullandığı iddia ediliyor. Bunun doğrudan bir kanıtı yoktur. Bu örneklerin belki de en ünlüsü Vitruvius Adamı'dır. Ancak bu tablodaki oranlar altın oranla eşleşmiyor. Nitekim Leonardo, çalışmalarında sadece tam sayı oranlarından bahsetti. Resimlerinde görülen altın oranın varsayılan örnekleri, doğada oranı bulanlarla aynı sınıftadır.

Devlin, altın oranın "popülerleşmesini", altın oranın hem doğanın hem de sanatın alemlerinde güzellik ve bütünlüğü büyük bir ruhsal ideal olarak, kozmik veya bireysel, organik veya inorganik, akustik veya optik, tüm yapılar, formlar ve orantıların süzülüşü olduğunu [...] tasvir eden evrensel bir yasa olduğunu savunan 19. yüzyıl Alman psikolog Adolf Zeising'e atfediyor. Bu sadece (yukarıdaki gibi) sahte kalıpları görmenin bir örneğiydi. Bununla birlikte, Zeising'in çalışması başkalarını etkilemeye devam etti ve modern mitin çoğunun temellerini attı.

Bu mitin bir başka örneği, altın oranın Atina'daki Akropolis'in bir parçası olan Parthenon'un oranlarında ortaya çıktığı iddiasıdır.

Yunan biliminde bunun bir kanıtı yoktur ve Partenon'un altın oran tarafından verilen oranlara sahip olduğu fikri sadece 1850'lere dayanmaktadır. Dahası, dikdörtgen seçiminize dikkat etmezseniz, Parthenon'un gerçek ölçüleri özellikle altın orana yakın oranlar vermez. Aslında, Parthenon uyumlu görünümünü, paralel gibi görünen ancak aslında yakınsayan veya eğrilen çizgilerin akıllıca konuşlandırılmasından alır, bu nedenle kesin oranlar vermek için yeterince hassas ölçümler almak neredeyse imkansızdır. Parthenon'un oranları yüksekliğine göre değiştiğinden, altın oranla uyumlu genel bir oran bulmak mümkün değildir.

Aynı şey Yunan mimarisinin geri kalanı için de geçerlidir: Yunanlıların altın oranı estetik olarak hoş gördüklerine ya da sanatlarında ve mimarilerinde kullandıklarına dair hiçbir kanıt yoktur.

Bu müzik için de geçerlidir. Altın oranın müzikal kompozisyonda önemli olduğu iddia edilmektedir. Bunun çok az kanıtı var. Ancak kompozisyonda önemli olan ölçektir ve ölçek 2'nin on ikinci dereceden kökü ile çok yakından bağlantılıdır. Müziğin kalbinde yer alan altın oran değil bu ikinci sayıdır.

Altın oran hakkındaki bu kalıcı mitlerde çok gerçek bir tehlike var. Okuldaki öğrenciler ve daha pek çoğu, matematiğin çalışma şekli hakkında sahte bir gerçekle kandırılıyor. Er ya da geç bu gerçekliğin doğru olmadığını bulacaklar ve matematiğin dünyayı açıklama yeteneğine olduğu inancını kaybedecekler.

Büyük gerçeklik

Altın oran konusunda oldukça dışlayıcı olmaktan ziyade altın oranın gerçekten ne kadar şaşırtıcı olduğunu vurgulayarak bu bölümü bitirmek istiyorum - gerçekten de özel olmak için tüm bu sahte iddialara ihtiyaç duymuyor.

İlk olarak, altın oranla gerçekten ilgili olan doğal fenomenlere dönelim. Altın oran, ünlü Fibonacci dizisi ile yakından ilgilidir.

\( 1, 1, 2, 3, 5, 8, 13, 21, ... \)

Fibonacci dizisi hem popülasyonların büyümesi hem de şekillerin bir araya getirildiğiyle bağlantılı olduğundan kesinlikle doğada ortaya çıkar. Örneğin, bu dizi sıralı bir şekilde birbirine uyması gereken ayçiçeği üzerindeki sarmallarda ve en fazla güneş ışığını yakalamak için ayarlanması gereken bazı bitkilerin yapraklarında görülebilir. Sonuç olarak, bazı doğal fenomenlerde ortaya çıkan altın orana yakın oranları gözlemlemek mümkündür.

İrrasyonel sayılar, kesirler tarafından temsil edilemeyen ve yinelenen bir öbekle bitmeyen sonsuz ondalık sayı genişlemesine sahip sayılardır. Bu gerçek, doğada irrasyonel sayıları gözlemlemenin zor olduğu anlamına gelir. Altın oran, şaşırtıcı olarak hepsi içinde en irrasyonel sayı olma özelliğine sahiptir. Bu, sadece tam bir kesir gibi temsil edilmediği gibi, aynı zamanda bir kesirle kolayca yaklaşık olarak tahmin edilmesi bile mümkün olmadığı anlamına gelir.

Altın oranın bir kesirle yaklaşılabilmesindeki zorluk, senkronizasyon sürecini inceleyen matematikçiler ve bilim adamları için onu çok yararlı bir sayı yapar. Bu, doğal frekanslı bir sistem farklı bir frekanstan biri tarafından zorlandığında ve zorlama frekansını benimsediğinde ortaya çıkar. Bir örnek, insan vücudunun günlük güneş ışığı frekansıyla senkronizasyonudur. İkinci bir örnek, Güneş'in çevresindeki yörüngenin doğal döngülerine senkronize olan Dünya iklimidir.

Bununla birlikte, senkronizasyonun kendisi bir problem olabilir, bu da bir sistemde istenmeyen rezonanslara yol açar (bir yürüyen bant üzerinde dolaştığında şiddetli bir şekilde titreşen bir asma köprü gibi). 1/ϕ oranında iki frekans seçerek, altın oranın aşırı irrasyonalitesi sayesinde senkronizasyonu önleyebiliriz. Bu çok yararlı özellikten, beyin ve böcek türleri aynı zamanda iklim bilimciler ve hatta uçak üreten insanlar tarafından faydalanılıyor gibi görünüyor.

Yani altın oranın oynadığı bir rol var, ancak onunla ilişkili mitolojide sık sık okuduğunuz gibi bir rol değil. Ne yazık! Çok hoş bir paradokstur ki altın oran ile ilgili en ilginç şey bir oran olmadığıdır.

Kaynak:

Plus Magazine, Chris Bud, Myths of maths: The golden ratio, https://plus.maths.org/content/myths-maths-golden-ratio