“Görelilik” Üzerine: Ne Anlaşılıyor, Ne Anlamalıyız?
On "Relativity": How is it perceived? How should we perceive?
Mehmet Ali Olpak
Dr., Türk Hava Kurumu Üniversitesi Mühendislik Fakültesi
[email protected] Özet
Genellikle Albert Einstein’ın adıyla anılan görelilik kuramları ve “görelilik” kavramının bizzat kendisi modern fizikte çok önemli bir yer tutmaktadır. Çeşitli bilim ve felsefe dallarının literatürlerinde de görelilik kavramına sıkça başvurulmakta, ayrıca Einstein’ın adıyla anılan kuramlara yapılan çok çeşitli atıflara da rastlanmaktadır. Literatürde kavramın çağrıştırdığı “değişkenlik” ve “öznellik” gibi başka kimi kavramlarla ilişkisinin öne çıktığı sıkça görülse de, fizik literatüründe göreliliğin esasen “fizik yasalarının nesnelliğine” ve “fiziksel gerçekliğin biricikliğine” vurgu yapan bir kavram olduğu iddia edilebilir. Bu çalışmanın amaçlarından biri, söz konusu iddiayı savunan bir yaklaşımla görelilik kuramlarını izah etmektir. Bu sayede “hareketin göreliliği” olgusunun fizik bilimi içerisinde nasıl ele alındığının yaygın olarak anlaşılması umulmaktadır.
Bu çalışmanın başka bir amacı da, görelilik kuramlarının genel anlamda materyalist görüşlerin altını oyduğu, akla ve modern bilime dayalı bir gerçeklik algısının ve bunlara yaslanan felsefi yaklaşımların geçerliliğini yitirdiği gibi iddialara karşı göreliliğin “neden bu işe yaramayacağını” açıklamaya çalışmaktır. Ayrıca, söz konusu iddiaların hususi hedefleri arasında yer alan diyalektik materyalizmin bu tartışmanın neresinde durduğuna dair bir görüş öne sürülecektir.
Anahtar kelimeler: Görelilik kuramı, Galileo’cu görelilik, Einstein’cı görelilik, hareket kuramı Abstract
The theories of relativity, which are generally named after Albert Einstein, and the concept of “relativity” itself occupy a very important position in modern physics. It is observed that in the literature of numerous branches of science and philosophy the concept of relativity is frequently cited, and furthermore, various citations to the theories named after Einstein are also observed. Although the relation between the relativity concept and concepts like “variability” and “subjectivity” is frequently seen to be prominent in the literature, it can be asserted that the concept of relativity in the physics literature is one which emphasizes the “objectivity of the laws of physics” and the “uniqueness of physical reality”. One aim of this study is to explain the theories of relativity with an approach which supports this assertion. This way, it is hoped, how the phenomenon of “relativity of motion” is considered within the science of physics will be widely understood.
Another aim of this study is to try to explain, against assertions that the theories of relativity undermine materialist views in general, that a perception of reality relying on reason and modern science and also philosophical approaches depending on this perception have lost their validity, why relativity “is useless to support these assertions”. Furthermore, an idea will be put forward on where dialectical materialism, which is among the specific targets of these assertions, stands within this discussion.
Key words: Theory of relativity, Galilean relativity, Einsteinian relativity, theory of motion
Giriş
Kimileri için âdet olduğu üzere, görelilik ile ilgili bir anlatıya başlarken söylenecek ilk söz, hareketin göreliliği fikrinin Einstein ile ortaya çıkmadığıdır. Hareketin göreliliği Newton’cu fizikte de mevcuttur (örneğin, bkz. Rindler, 2006: 13), fakat görelilik ilkesinin içeriği farklıdır. Dolayısıyla, ilk etapta açıklığa kavuşturulması gereken konu, görelilik ilkesinin içeriği olmalıdır. Bunu yaptıktan sonra, Newton’cu fizikten Einstein’cı fiziğe geçişte nelerin değiştiği, nelerin değişmediği daha açık bir şekilde ve nicel olarak tarif edilebilir.
Görelilik ilkesinin içeriğinde anlaşıldıktan sonra, iki başlığın tartışmaya açılması gerekir. Bunlardan bir tanesi, bu içeriğin ne tür felsefi yorumlara izin verdiği, ne tür yorumlara izin vermediğidir. İkincisi ise, daha genel bir bağlamda, “bugünkü anlamıyla fizik bilimi”nin “bugünkü anlamıyla felsefe” ile ilişkisidir. Bu noktaya gelindiğinde, bu noktaya kadarki tartışmanın fizik bilimine katkı sunmak açısından çok da gerekli olmadığının, ancak güncel entelektüel atmosferdeki çeşitli yorum hatalarını temizlemeye yarayacağının görülmesi ilginç olacaktır.
1. Galileo’cu görelilik
1.1. Kopernik’in evren modeli ve Galileo’nun fikirleri
Hareketin göreliliği fikri, bilim tarihinde önemli yer tutan bir dizi tartışmanın parçasıdır. Söz konusu tartışmaların en önemli dönüm noktası olarak, Batlamyus’un Dünya merkezli astronomisine karşı Kopernik’in Güneş merkezli astronomisinin ortaya çıkması gösterilebilir. Güneş merkezli bir astronomi modeli ilk kez Kopernik ile ortaya çıkmamıştır ve böylesi bir astronomi anlayışını işaret edecek fikirlerin Kopernik’ten önce de çeşitli entelektüel merkezlerde ele alındığını gösteren veriler mevcuttur (Bernal, 2008: 221). Yine de, bu astronomi yaklaşımının ortaya konmasında Kopernik’in katkısını öne çıkarmak anlamlıdır; zira o dönemde savunulması çeşitli nedenlerle zor olan bir hipotezi ortaya atma bağlamında Kopernik cesaret göstermiştir (Bernal, 2008: 335).
Kopernik’in modeli, Katolik dünyasındaki egemen görüşe muhalefet eden cesur bir tutumun ürünü olmakla birlikte, söz konusu egemen görüşle önemli bir ortaklığı vardı: Gök cisimleri arasında bir hiyerarşi tarif etmesinin yanında, halen gezegenlerin çembersel yörüngelerde hareket etmesi gerektiğini ileri sürüyordu [1] ve de hem yerde hem gökte aynı fizik yasalarının geçerli olduğu düşüncesini içermiyordu. İkinci konu Newton’a kadar bilim literatüründe vücut bulmayacaktı; dolayısıyla şimdilik onu bir kenara bırakabiliriz. Görelilik tartışması açısından önemli olan unsur, göksel cisimler arasındaki hiyerarşidir. Evrenin merkezinde ve mutlak şekilde durduğu iddia edilen bir cismin varlığı, Batlamyus’çu ve Kopernik’çi görüşler tarafından paylaşılmaktadır (Bernal, 2008: 356). Kopernik, kendine göre çeşitli nedenlerle bu cismin Güneş olması gerektiğini ileri sürmüştür.
Gök cisimleri arasındaki hiyerarşiyi hem fikren, hem teknik anlamda ortadan kaldırmak, Einstein’ın genel görelilik kuramına kadar mümkün olmadı. Ancak Galileo’nun fikirleri, bu hiyerarşiyi fikri anlamda tamamen, teknik olarak da kısmen ortadan kaldırmaya yetecekti.[2]
Galileo, Kopernik modelinin önemli savunucularından biriydi (Bernal, 2008: 371). Ama bu modelin çok ötesine geçen fikirler öne sürdü. Söz konusu fikirlerin gelişiminde Galileo’nun deneyleri ve kendi teleskobu yardımıyla gök cisimleri üzerinde yaptığı gözlemlerin etkili olduğu açıktır. Galileo’nun en meşhur gözlemlerinden biri, Jüpiter’in uyduları üzerine yaptığı gözlemlerdir (Bernal, 2008: 371). Bir gezegen ve onun etrafında dönen uydular: Böylesi bir durumun Dünya’ya özgü olmaması, Dünya’nın düşünüldüğü kadar özel bir cisim olmadığı anlamına gelmeliydi.
Galileo’nun deneyleri sayesinde ulaştığı başka bir fikir de “eylemsizlik” fikriydi. Bu fikirle, durgun olan veya düz bir çizgi üzerinde sabit hızla hareket eden bir cisme herhangi bir kuvvet etki etmediği sürece cismin bu “hareket durumu”nu sürdürme eğiliminde olacağını iddia etti. Bu fikre, yaptığı deneyler yoluyla ulaşmıştı (Giancoli, 2008: 85). Galileo, cisimlerin hareketi üzerine Newton’un sonradan hareket kuramında birleştirileceği çeşitli fikirler üretmişti. Fikirlerini, yaptığı deneyler ve bu deneyleri matematiksel olarak ifade etme şeklindeki yöntemine dayandırıyordu (Bernal, 2008: 373-375); bugün de bilimsel yöntemin temeli olarak kabul edilen yönteme. Bu nedenle, kimi yazarlara göre modern bilimin miladı veya “bilimsel devrimin başlangıcı” Galileo’nun çalışmalarıdır (Stanford, 2017; ayrıca bu kaynaktaki atıflar incelenebilir).
Galileo’nun bu fikirlerini tutarlı bir kuram içinde tam olarak birleştirme noktasına ulaşamadığını biliyoruz. Bu işi Newton yapacaktı. Ancak, bizim tartışmamız açısından kritik olan mesele, hareketin göreliliği fikrinin ortaya çıkmış olmasıdır.[3] Newton’un hareket kuramı içerisinde birleştirilecek olan bu fikirler arasında hareketin göreliliği ilkesini Galileo’cu görelilik olarak anmamızın nedeni budur. Bu noktadan itibaren, tartışma Newton’un hareket kuramı çerçevesinde devam ettirilmelidir.
1.2. Newton’un hareket kuramı ve kütle çekim yasası
Newton’un hareket kuramı, ünlü hareket yasaları ile ifade edilir (Giancoli, 2008: 84-89; Rindler, 2006: 4):
Yasa 1: Bir cisim, üzerine hiçbir kuvvet etki etmediği sürece, durgun olma veya düz bir çizgi üzerinde sabit hızla hareket etme şeklindeki hareket durumunu korur.
Yasa 2: Bir cismin üzerine etki eden toplam kuvvet, cismin ivmesiyle doğru orantılı ve aynı yönlüdür. Kuvvet ve ivme arasındaki orantı sabiti cismin kütlesine eşittir.
Yasa 3: Bir cisim ikinci bir cisim üzerine bir kuvvetini uyguladığında, ikinci cisim de birinci üzerine aynı büyüklükte ve ters yönde bir kuvvet uygular.
Yukarıdaki ifadeler, yasaların bir derste izah edileceği şekilde yazılmıştır. Ancak içeriği yeterli düzeyde ortaya koymaktadır. Yasaların bir özelliği, öncelikle “noktasal parçacıklara” uygulanacak şekilde ifade edilmiş olmalarıdır. Newton, ve astronomi ile ilgilenen tüm bilimciler için, uzakta küçük noktalar şeklinde görünen gök cisimlerini böyle bir soyutlamayla ele almak pek tabii ki mantıklıydı. Yasaların uygulanabilmesi için gerekli olan matematik de, bizzat Newton (ve bağımsız olarak Leibniz) tarafından icat edildi: “calculus”. Bu sayede, cisimleri noktasal parçacık olarak soyutlamadan da yasaları uygulama olanağı elde edildi. Elbette bunun için, sonlu hacimler işgal eden cisimleri sonsuz küçük hacimler işgal eden noktasal parçalara bölerek incelemek gerekiyordu. Bu yaklaşım, icat edilen matematik bilgisinin de temelini oluşturmaktadır.
Görüldüğü gibi, birinci yasa, doğrudan Galileo’nun ifade ettiği haliyle eylemsizlik ilkesidir. Peki, görelilik ilkesi nerede durmaktadır? Bu sorunun yanıtı, başka bir soruyla ilişkilidir: Bir cismin üzerine kuvvet etki edip etmediğinden nasıl emin olacağız?
Newton’un kendisinin de bu soruya felsefi anlamda tatmin edici bir yanıt verebildiğini sanmıyorum. Ancak, kuvvetlerin fiziksel kaynağının bizzat maddenin kendisi olması gerektiğini Newton da kabul ediyordu diyebiliriz; zira hem kütle çekim yasası, hem de dönemin mekanik bilgisinde içerilen kuvvet türlerinin tamamı, kimin kuvveti incelediğinden bağımsız olarak bir maddi kaynakla ilişkilendirilebilen türdendi (böyle olmayan “hayali kuvvetlere” değineceğiz)[4]. Dolayısıyla, bir kuvvetin varlığından söz etmeyi gerektirecek tüm kaynaklardan uzakta bulunan cisimlerin, hiçbir kuvvetin etkisi altında olmadığı düşünülebilirdi (Rindler, 2006: 4). İşte böylesi cisimler, eylemsizlik yasasının gerektiği şekilde hareket ederlerdi ve “eylemsiz” olarak nitelediğimiz bu cisimlerden birinin üzerine oturup, çeşitli kuvvetlerin etkisi altındaki başka bir cismi incelemek istediğinizde Newton’un hareket yasaları size incelenen cismin nasıl hareket edeceğini hesaplama yeteneği kazandırırdı. Dahası, eylemsiz cisimlerin hepsi, çeşitli kuvvetlerin etkisi altındaki başka bir cisme etki eden tüm kuvvetleri aynı görmelidir; işte bu nokta, görelilik ilkesinin devreye girdiği yerdir. Newton’un hareket kuramı Galileo’cu göreliliğe uyar. Buna göre, evrendeki tüm eylemsiz gözlemciler birbirine denktir; birbirlerine göre mutlak bir durgunluk veya hareketlilik durumu tarif edilemez ve birbirlerini eylemsiz olarak görürler. Ayrıca her gözlemci (eylemsiz olsun veya olmasın), kendisini durgun olarak görür. Bunların bir sonucu olarak, evrendeki tüm eylemsiz gözlemciler, bir cismin üzerine etki eden net kuvveti ve o cismin ivmesini aynı şekilde görür.[5] Bu son argümanı birazdan açıklayacağız.
Şimdi, yukarıda dile getirilen fikirleri, sözünü ettiğimiz matematiği kullanarak ifade etmeye başlayabiliriz. \(G_1\) ve \(G_2\) gibi iki gözlemcimiz olsun. İki gözlemci de belirli bir cismi inceliyor olsun. Örneği basitleştirmek adına, incelenen cismin bir doğru üzerinde hareket ettiğini varsayalım. \(G_1\) ve \(G_2\)’nin her ikisinin birer saati ve birer cetveli olsun. Saatler, sırasıyla, \(t_1\) ve \(t_2\) değişkenleriyle temsil edilsin. Cetveller de, sırasıyla, \(t_1\) ve \(x_2\) değişkenleriyle temsil edilsin. Bu durumda, cismin \(G_1\)’e göre herhangi bir \(t_1\) anındaki konumuna \(x_1\) (\(t_1\)), \(G_2\)’ye göre herhangi bir \(t_2\) anındaki konumuna \(x_2\) (\(t_2\)) deriz. Burada parantez içindeki \(t_1\) ve \(t_2\) değişkenleri bağımsız değişkendir, \(t_1\) ve \(x_2\) değişkenleri de bunların fonksiyonu olur.[6]
Galileo’cu göreliliğin ilk adımı, saatleri ayarlama üzerine olacaktır. Her iki gözlemciye de özdeş birer saat verebiliriz. Özdeşlik, saatlerin tik-tak sıklığının aynı olması anlamına gelir. Saatleri belirli bir anda senkronize de edersek, aynı tik-tak sıklığıyla çalışacakları için saatler hep aynı değeri okur. Dolayısıyla, \(t_1=t_2≡t\) şeklinde ortak bir zaman değişkeni tanımlayabiliriz.
Devam etmeden önce, bir not düşmek faydalı olacaktır: Burada bir varsayım daha yapıldı. Saatlerin tik-tak sıklığının veya birinin tik-taklarını diğerinin nasıl duyduğunun, saatlerin birbirine göre hareket durumundan bağımsız olduğunu varsaydık. Bu varsayım, konum değişkenleri için de yapılıyor. Einstein’cı göreliliğin eleştirdiği de tam olarak bu varsayımlar olacak. Ayrıca bu varsayımlar, herkes için geçerli evrensel zaman ve konum değişkenlerinin varsayılmasını zorunlu kılar ki, Newton’cu fizikte bir mantıksal zorunluluk olarak “mutlak zaman” ve “mutlak uzay” kavramları bu yüzden vardır. Mutlak zaman, monoton bir şekilde “ileri” doğru akan bir zaman değişkenidir ve bir nevi evrensel saat olarak düşünülebilir. Mutlak uzay ise, maddenin yokluğunda bile “uzayın kendisinin var olduğu” iddiasına tekabül eder. Daha önemli olan bir varsayım ise şudur ki, böyle bir kusursuz boşluğun “doğal” koordinat sistemi Kartezyen olmalıdır; bu durum uzayın geometrisinin Öklidyen olduğu varsayımına karşılık gelir (Rindler, 2006: 4). Dolayısıyla Galileo’cu görelilik ilkesi, tüm eylemsiz gözlemciler için bir evrensel saatin ve bir evrensel Kartezyen koordinat sisteminin tanımlı olduğunu varsayar. Bir eylemsiz gözlemcinin saati ve koordinat sistemi, bu evrensel saat ve koordinat sistemine atıfla ayarlanabilir. Dolayısıyla, Galileo’cu görelilik ilkesi uyarınca, tüm eylemsiz gözlemciler iki an arasındaki farkı (zaman aralığını) aynı görür. Benzer şekilde, tüm eylemsiz gözlemciler iki nokta arasındaki mesafeyi aynı görür. Bu noktalara ileride tekrar değineceğiz.
Kaldığımız yerden devam edelim. Her iki gözlemci için ortak bir saat tanımladığımıza göre, artık incelenen cismin \(G_1\) ve \(G_2\)’ye göre konum fonksiyonlarını \(x_1(t)\) ve \(x_2(t)\) olarak yazabiliriz. Şimdi bu fonksiyonların birbiriyle ilişkisini inceleyelim. Bunun için, \(G_1\) ve \(G_2\)’nin birbirlerine göre hareket durumlarını da ele almamız gerekecek. Örneğimizi basitleştirmek adına, \(G_1\)’in eylemsiz olduğunu varsayalım. \(G_2\)’nin eylemsiz olduğu ve olmadığı durumların sonuçlarını ayrı ayrı göreceğiz.
\(G_2\)’nin \(G_1\)’e göre konumuna \(x_{2,1}(t)\) dersek, \(x_1(t)=x_2(t)+x_{2,1}(t)\) olur. Temel kinematik bağıntılar uyarınca, bir konum fonksiyonunun zamana göre birinci türevi hız fonksiyonu, ikinci türevi ise ivme fonksiyonudur. Birinci zaman türevlerini \(\dot{x}\), ikinci türevleri de \(\ddot{x}\) şeklinde ifade edersek [7], şu bağıntıları elde ederiz:
$$\dot{x}(t)=\dot{x}_2(t)+\dot{x}_{2,1}(t) ; \ddot{x}(t)=\ddot{x}_{2,1}(t).$$
\(\dot{x}_1(t)\) ve \(\ddot{x}_1(t)\), sırasıyla, cismin \(G_1\)’e göre hızı ve ivmesidir. \(\dot{x}_2(t)\) ve \(\ddot{x}_2(t)\), sırasıyla, cismin \(G_2\)’ye göre hızı ve ivmesidir. \(\dot{x}_{2,1}(t)\) ve \(\ddot{x}_{2,1}(t)\) ise, sırasıyla, \(G_2\)’nin \(G_1\)’e göre hızı ve ivmesidir. \(G_2\)’nin eylemsiz olup olmadığı burada devreye girmektedir. \(G_2\)’nin eylemsiz olması demek, üzerine etki eden net kuvvetin sıfır olması anlamına gelir. Dolayısıyla, Newton’un ikinci yasası uyarınca, \(G_2\)’nin net ivmesi de sıfır olmalıdır yani \(\ddot{x}_{2,1}(t)=0\) olur. Aksi halde, yani \(G_2\)’nin eylemsiz olmaması durumunda \(G_1\) ve \(G_2\) incelenen cismin ivmesini farklı görecek, dolayısıyla cisme etki eden net kuvvetleri de farklı okuyacaklardır. Ancak kuvvetlerin, gözlemciden bağımsız maddi kaynaklarla ilişkilendirilebilmesi gerektiğini söylemiştik. Dolayısıyla, \(G_2\)’nin “gerçekte var olmayan” kuvvetler göreceğini anlarız. Bunlara “hayali kuvvet” denir. Bu durumu, ani fren yapan bir araçta yaşadığınız ileri doğru savrulma hissiyle örneklendirebiliriz. Araç fren yaptığında, hissedilir bir ivmeyle yavaşlamaya başlar; aracın ivmesi ile hızı ters yönlüdür. Ancak araçta oturan insanların önünde bir engel yoksa (veya aracın yavaşlama kuvvetini insanlara ileten bir mekanizma yoksa), insanlar öne doğru savrulacaktır, bu durum eylemsizlik ilkesinin açıkladığı durumdur. Savrulan kişi bir engele temas ettiğinde savrulması durur ve kişi kendisini öne doğru ittiren bir kuvvet varmış gibi hisseder. Ama fiziksel olarak var olan kuvvet geriye doğrudur. Kişinin öne doğru bir kuvvet varmış gibi hissetmesinin nedeni, her gözlemcinin kendisini durgun görmesi ve bu durumda kişinin eylemsiz olmayan bir gözlemci olmasıdır.[8]
Şimdi, \(G_2\)’nin eylemsiz olduğu duruma geri dönebiliriz. Bu durumda, bağıntılarımız şöyle olur:
$$\dot{x}_1(t)=\dot{x}_2(t)+\dot{x}_{2,1}(t) ; \ddot{x}_1(t)=\ddot{x}_2(t).$$
Yani, bir cismin ivmesi[9], her iki gözlemci için de aynıdır. Gözlemcilerimiz üzerinde eylemsiz olma hali dışında bir koşul olmadığına göre, cimin ivmesi tüm eylemsiz gözlemciler için aynıdır! İşte bu nedenle, evrendeki tüm eylemsiz gözlemciler için, evrenin evrimini belirleyen temel kanunlar, burada Newton’un hareket yasaları, aynı şekilde işler. Yani, Galileo’cu görelilik, maddi gerçekliğin tarifine dair bir keyfiyeti değil, “gözlemciden bağımsızlığı” ifade eder: Maddi gerçeklik, bir eylemsiz gözlemciden diğerine değişmemektedir; yani gözlemciden bağımsızdır. Bu anlamda, görelilik ilkesi, bir tür “değişmezliğin”[10] ifadesi olarak da anlaşılabilir.
Daha sonra tekrar değineceğiz, ancak burada da vurgulamakta fayda var: Farklı gözlemcilerin fiziksel olayların gerçekleştiği noktalara ve anlara farklı koordinat (konum ve zaman) değerleri ataması, maddi gerçekliğin gözlemciye bağlı olduğu şeklinde yorumlanabilmektedir. Bu yorum genelde Einstein göreliliği üzerinden yapılıp, “nesnel gerçeklik düşüncesinin” altını oyduğu iddia edilmektedir. Burada iki saçmalık mevcuttur: 1) Bu bir keyfiyetse, bizzat Newton’cu fizikte zaten vardır; 2) görelilik ilkesi, fizik yasalarını gözlemcilerden bağımsız ifade etmenin yolunu göstermekte olduğu halde tam olarak tersten okunmaktadır.
Buraya kadar, Galileo’cu görelilik ilkesinin Newton’un hareket yasaları ile ilişkisi üzerinde durduk. Bu noktada, konunun Güneş merkezli evren modeli ile ilişkisini de açıklayabiliriz.
Newton’un üçüncü yasası uyarınca, her kuvvete eşlik eden eşit büyüklükte ve zıt yönde bir ikinci kuvvet vardır. Örneğin Güneş Dünya’yı belirli bir F kuvveti ile çekiyorsa, Dünya da Güneş’i -F kuvveti ile çekmektedir. Bu ilişki her an ve kesin olarak geçerlidir. Dolayısıyla, Dünya ile Güneş arasındaki hareket ilişkisine nereden baktığınızın önemi yoktur.
Newton’un hareket yasaları, burada bırakırsak, Batlamyus’çu evren modeline olduğu kadar Kopernik’çi evren modeline de muhalefet eden bir görüntü sergiler. Ancak, pratik olarak da söyleyebiliriz ki, bazı referanslar diğerlerinden daha berrak bir görüntü sunmaktadır. Örnek olarak, belirli bir yükseklikten serbest bırakılan bir cismin hareketini ele alalım. Genelde böylesi bir durumda “cisim yere düşer”. “Dünya zıplayıp cisme çarptı” demeyiz. Bunun nedeni nedir? Bunun nedeni, kuvvet ilişkisi tamı tamına demokratik olsa da kütlesi büyük olan cismin daha az kıpırdayacak olmasıdır. Bunu izah etmek için, Newton’un ikinci yasasını ve kütle çekim yasasını kullanabiliriz.
Newton’un kütle çekim yasası şöyle özetlenebilir: \(m_1\) ve \(m_2\) kütlelerine sahip iki noktasal cisim, birbirlerinden r kadar uzakta iken, aralarındaki kütle çekim kuvveti cisimleri birbirine doğru çekecek şekildedir ve cisimlerin kütleleri ile doğru, aralarındaki mesafenin karesi ile ters orantılıdır. Yani: \(F∝ \frac{m_1 m_2}{r^2}\). Bunu bir eşitlikle ifade etmek istediğimizde, orantı sabiti olarak “Newton sabiti” olarak adlandırılan bir sayı bağıntıya dâhil olur: \(F=G\frac{m_1 m_2}{r^2}\) (burada \(G\) Newton sabitidir). Bu bağıntıda yön bilgisini vermeden, kuvvetin büyüklüğünü yazmış olduk. Kuvvetin yönlü (vektörel) bir nicelik olduğunu unutmamak gerekir; bu bilgiyi birazdan kullanacağız. Şimdi kütle çekim yasasını ikinci hareket yasası ile birleştiren bir örnekte, Einstein’ın tabiriyle bir “düşünce deneyi” yapalım.
\(m_1\) ve \(m_2\) kütlelerine sahip iki noktasal cismi, uzayda başka kuvvet kaynaklarının olmadığı bir ortamda \(A\)ve \(B\) olarak adlandırdığımız iki noktaya yerleştirelim ve ilk hız vermeksizin serbest bırakalım; serbest bıraktığımız anı da t=0 olarak seçelim:

Cisimlerin herhangi bir t anındaki konumlarına \(x_1(t)\) ve \(x_2(t)\) demiş olduk. Cisimler, kütle çekim kuvvetinin etkisiyle birbirlerine doğru hareket edeceklerdir. Kütleçekim kuvvetleri ilk andan itibaren ve her zaman cisimleri birleştiren doğru boyunca uzanacaktır; ilk hız da vermediğimiz için, cisimlerin A ve B noktalarını birleştiren doğru boyunca hareket edip bir noktada kafa kafaya çarpışmalarını bekleriz.[11] Bu olayın gerçekleşmesini beklediğimiz noktaya \(x_b\) adını verdik (“buluşma noktası”). Bu olayın hangi anda gerçekleşeceğini bulmak için hareket yasalarının vereceği denklemi çözmek yeterli olacaktır. Ancak bizim bu bilgiye ihtiyacımız olmayacak. Değerinin ne olduğunu önemsemeksizin, çarpışmanın gerçekleşeceği ana \(t=t_b\) dersek, \(x_1 (t_b)=x_2 (t_b)=x_b\) bilgisini elde ederiz. Bunu not edelim.
Newton’un kütle çekim yasası ile ikinci hareket yasasını birlikte kullandığımızda şu denklemleri elde ederiz:
$$\frac{Gm_{1}m_{2}}{(x_{1}(t)-x_{2}(t))^{2}}=m_{1}\ddot{x}_{1}(t) ; -\frac{Gm_{1}m_{2}}{(x_{1}(t)-x_{2}(t))^{2}}=m_{2}\ddot{x}_{2}(t)$$
x ekseninde sağa doğru olan yönü pozitif yön olarak kabul ettik; \(m_1\) kütleli cisme etki eden kuvvet bu yöndedir. Kuvvet ifadesindeki faktörlerin her biri pozitif sayıdır, \(m_1\) kütleli cisme etki eden kuvvetin x-bileşeni de pozitiftir. Aynı gerekçelerle, \(m_2\) kütleli cisme etki eden kuvvet negatif yönlü olduğu için x-bileşeni negatiftir. Denklemlerde bunları görüyoruz. Cisimlerin herhangi bir t anındaki konumları \(x_1(t)\) ve \(x_2(t)\) olduğuna göre ve cisimler düz bir doğru boyunca hareket edeceğine göre, herhangi bir t anında aralarındaki mesafenin karesi \((x_1(t)-x_2(t))^2\) olur.
Bu diferansiyel denklemleri çözüp \(x_1(t)\) ve \(x_2(t)\) fonksiyonlarını hesaplamak çok da kolay bir iş değildir. Ancak, denklemlere biraz dikkatli bakınca ilginç bir bilgiye ulaşırız:
$$\frac{Gm_{1}m_{2}}{(x_{1}(t)-x_{2}(t))^{2}}=m_{1}\ddot{x}_{1}(t)=-m_{2}\ddot{x}_{2}(t) => \frac{\ddot{x}_{1}(t)}{m_{2}}=-\frac{\ddot{x}_{2}(t)}{m_{1}} => \frac{x_{1}(t)}{m_{2}} =-\frac{x_{2}(t)}{m_{1}}+ at + b.$$
Zamana göre ikinci türevleri birbirine eşit olan iki fonksiyon arasındaki fark, en fazla, zamana göre ikinci türevi sıfır olan bir fonksiyon kadar olabilir (bu argümanı ispatlamak hoş bir egzersiz olur). Burada aradaki farkı temsil eden fonksiyonun parametreleri olan a ve b sayılarını belirlemek için, deneyimizin başlangıç koşullarını kullanmamız gerekir. t=0 anında cisimlerin konumları \(x_1(0)\) ve \(x_2(0)\) idi. Dolayısıyla, son bağıntıda t=0 koyduğumuzda şunu elde ederiz:
$$\frac{x_{1}(0)}{m_{2}}=-\frac{x_{2}(0)}{m_{1}}+b ⇒b=\frac{x_{1}(0)}{m_{2}}+\frac{x_{2}(0)}{m_{1}}$$
Bu şekilde, b sayısını başlangıç koşulları cinsinden bulmuş olduk. a sayısını bulmak için ise, cisimlerin ilk hızlarını kullanabiliriz. Koordinat fonksiyonları arasındaki bağıntının her iki tarafının zamana göre birinci türevi hız fonksiyonları arasındaki bağıntıyı verecektir:
$$\frac{\dot{x}_{1}(t)}{m_{2}}=-\frac{\dot{x}_{2}(t)}{m_{1}}+a$$
Cisimlerin ikisinin de ilk hızı sıfır olduğuna göre, a=0 sonucunu elde ederiz. Dolayısıyla, cisimlerin koordinat fonksiyonlarının zamana göre açık ifadelerini hesaplamamış olsak da, aralarındaki ilişkiyi hesaplamış olduk. Çarpışma anında \(x_1(t_b)=x_2(t_b)=x_b\) olacağına göre, şu bağıntıyı elde ederiz:
$$\frac{x_{b}}{m_{2}}=\frac{x_{b}}{m_{1}}-\frac{x_{1}(0)}{m_{2}}+\frac{x_{2}(0)}{m_{1}}$$
Görüyoruz ki, buluşma noktası ilk konumların arasındadır (beklendiği üzere), ve ilk konumlardan hangisine daha yakın olduğu, kütleler arasındaki ilişkiye bağlıdır. Örneğin, \(m_2\) \(m_1\)’e kıyasla çok büyük olduğunda, \(x_b\) konumu B noktasına çok yakın olacaktır. Aynı analizi, noktasal cisimlerle değil de sonlu hacimler kaplayan cisimlerle de yapabiliriz. Örneğin \(m_2\) kütleli cismi Dünya, \(m_1\) kütleli cismi de havadan serbest bırakılan bir taş olarak ele alırsak, çarpışma noktasının Dünya’nın yüzeyinin ilk anda bulunduğu yere çok yakın olması gerektiğini görürüz. Gündelik hayat nesneleri açısından bakarsak, Dünya’nın yerinden kıpırdamadığını varsaymak çok makul bir yaklaştırmadır. Benzer şekilde, Dünya’nın Güneş etrafındaki hareketi açısından da, Güneş’in yerinden kıpırdamadığı bir model kullanarak hesap yapmak yeterince makul bir yaklaştırma olur.
Newton’un hareket kuramına kadarki astronomi görüşlerinin temel eksiği, cisimlerin hareket örüntülerini hesaplamaya yarayan yasalardan yoksun olmalarıdır; “gezegenlerin yörüngeleri şu şekildedir” veya “gezegenler Güneş etrafında dönmektedir” gibi yarı ampirik yasalar ile işleyen sistemlerden söz edilebilir. Modern literatürde böylesi sistemler kurma ve çalışmaya “fenomenoloji” deniyor.[12] Newton ise bir kuram oluşturmuştur. Kuramın temel yapıtaşları Galileo’cu görelilik ilkesi ve Newton’un hareket yasalarıdır.
Newton’un başka bir katkısından daha söz etmek mümkündür. Kendisi, bu görüşlerini açıkladığı ünlü eserine “Doğa Felsefesinin Matematiksel İlkeleri” (Philosophie Naturalis Principia Mathematica) (Bernal, 2008: 426) adını vermişti. Onunla beraber, “doğa bilimi” ile “doğa felsefesi”nin bir anlamda özdeşleştiği iddia edilebilir. Fizik bilimi özelinde ele alırsak, “doğa felsefesi”nden anlaşılması gereken, yukarıdakine benzer bir matematiksel yaklaşımdır. Yasalar ifade edildikten sonra üretilecek tüm argümanlar, matematiksel olarak işleyen bir çıkarsamanın ürünü olmak zorundadır. Bu yaklaşımın zaman içinde diğer bilim dallarında da yaygınlaştığını ifade edebiliriz. Ancak daha önemli olan nokta şudur: Newton’un matematiksel fiziği ile birlikte, felsefi muhakemeler kuramların başlatıcısı olmaktan çıkmış, kuramların yorumlanmasına indirgenmiştir.[13] Bunun iyi veya kötü olarak değerlendirilmesi başka bir konu; ancak bir olgu olarak önemsenmesi gerekmektedir. Newton’un zamanından günümüze kadar ulaşmış ve bilim camiasında halen çok etkili olan pragmatik tutum esasen buradan beslenmektedir. Kuramlar, sağladıkları teknik beceri oranında değerlidir; felsefi anlamda gelişkinlik veya tutarlılık düzeyleri oranında değil. Bu yaklaşımın iktisadi anlamda doğrudan sonuçları vardır. Örneğin Newton’un hareket kuramı, bu yaklaşımla birlikte, öncelikle denizcilik alanında önemli bir sıçramaya katkı sunmuştur (Bernal, 2008: 433). Kuramın kendi niteliği bu açıdan tek başına yeterli olamazdı; onu kullanarak çok çeşitli bilgileri üretecek ve iktisadi alana yansıtacak insanların, teoriyi kullanma özgürlüğüne sahip olmaları gerekirdi. Bu anlayış, Newton’un döneminde başlamış olmakla birlikte esasen 18. yüzyılda burjuvazinin bilim ile kurduğu ilişkinin temeline yerleşti; zira bilim, iktisadi ve siyasi beklentilere yanıt üretme potansiyeline sahip olduğunu göstermişti (Bernal, 2008: 430-502).[14]
Söz konusu yaklaşımın, yöntemsel açıdan da bir sonucu vardır. Yukarıda sözü edilen pragmatik tutumu paylaşıp paylaşmamaktan bağımsız olarak, modern doğa biliminde “kuram” denen yapının bir tür soyut makineye dönüşmüş olduğu iddia edilebilir. Makinenin özsel amaçları, eğilimleri vb. yoktur. Tüm makineler, teknik becerilerle tarif edilen ortak amaçlar doğrultusunda geliştirilir ve (üzerinde) çalışılır. Makineye soru sorulur, makine yanıt üretir. Elbette, bilgi üretiminin felsefi bir zeminden tamamen yalıtılması mümkün değildir. Böyle olsaydı, bu soyut makinelerin her durumda birbiriyle tutarlı felsefi yorumlara neden olmasını beklerdik. Böyle olmadığını biliyoruz. Ancak yine de, bu soyut makinelerin “anlamlı bir ilişki” kurabilecekleri farklı felsefi zeminlerin Newton’dan sonra sayıca epey azaldığını iddia etmek mümkündür.
2. Einstein’cı görelilik: Özel ve genel kuramlar
Galileo’cu görelilik ilkesi ve bunun Newton’un hareket kuramındaki işlevini tartışmış olduk. Bu noktada, Einstein’ın kuramlarını tartışmaya başlayabiliriz. Nereden kaynak aldılar, hangi sorunları çözdüler, başka nasıl sorunlar yarattılar? Einstein’ın kuramlarının incelenmesi, iki açıdan değerli görüşler sunacaktır. Birincisi, görelilik kuramları, fizik kuramlarının ortak bir metodolojik zeminde birbirini nasıl eleştirdiğinin ve aştığının değerli örneklerini sunar. Bu husus diyalektik materyalizm açısından özellikle önemlidir, zira bilimde bilgi üretme sürecinin mantığını[15] ortaya koymaktadır. İkinci olarak da, Einstein’ın kişisel felsefi motivasyonlarının ve bu motivasyonların fizik literatürüne yansımasının, felsefi ve ideolojik bağlamlarda materyalizme “fiziken” güç verdiğini göstermesi açısından değerlidir. Bilim insanlarının aydınlanmacı motivasyonlarla hareket etmelerini zorlaştıran ve halen içinde yaşadığımız siyasi iklimde bu desteğin çok değerli olduğu açıktır. Elbette, diyalektik materyalizm de bu destekten payını almıştır.
2.1 Özel görelilik kuramı veya göreliliğin özel kuramı
2.1.1 Elektromanyetizma kuramının yarattığı sorun
19. yüzyılın sonlarına doğru, kuramsal fizikte bazı sorunlar birikmeye başlamıştı. Aslında sorunların birikmediği bir dönemin varlığından bahsetmek olanaksızdır, ancak “çözülememiş zor problemler” zaman içinde bir bir çözüldüğü halde, bazı başlıklarda doğa o günkü fizik anlayışımıza karşı yapısal bir direnç gösteriyordu.
Özellikle 19. yüzyılın ikinci yarısında hızla gelişen elektrik endüstrisi, elektrik ve manyetizma konularında bilgi birikiminin hızla derinleşmesini motive etmişti. Fizik dünyası bu gelişimin gerisinde kalmadı ve 1864 yılında James Clerck Maxwell’in yayınladığı elektromanyetizma kuramı (Jackson, 2001: 1) ile önemli bir kuramsal zemine erişildi. Esasında elektromanyetizma kuramı, uzun bir geçmişe yayılan ve geometrik optik, elektrik ve manyetizma ile ilgili bir dizi çalışmanın Maxwell’in bazı özgün katkılarıyla birlikte toplanması ve bir “birleşik kuram”[16] altında ifade edilmesiydi. Kendi başına ilginç bir konu olarak elektromanyetizma kuramının gelişim süreci ve bu sürecin dönemin elektrik endüstrisi ile ilişkisini inceleme işini başka bir çalışmaya bırakmak zorundayız; burada, konunun görelilik ilkesi ile ilişkisini ele alacağız.
Elektromanyetizma kuramının dönem açısından en “can sıkıcı” özelliği, Galileo’cu görelilik ilkesine uymamasıydı (Jackson, 2001: 516)! Bu durumu klasik bir örnekle izah etmek mümkündür.
Tek düze bir manyetik alanın[17] bulunduğu bir bölgede, manyetik alan doğrultusuna dik bir düzlem boyunca uzanmış ve bu düzlemde rijit[18] bir şekilde hareket eden nötr bir metal çubuk düşünelim. Çubuk üzerine etki eden hiçbir kuvvet olmasın, bu şekilde çubuk eylemsiz olacaktır. Çubuk, başka bir eylemsiz gözlemciye göre sabit bir hız ile manyetik alana dik olan düzlemde yatay şekilde öteleniyor olsun. Durumu aşağıdaki şekilde görebiliriz:

Bir manyetik alanın var olduğu bir bölgede hareket halindeki yüklü parçacıklara manyetik kuvvetler etki eder. Parçacık herhangi bir noktadan geçerken üzerine etki eden manyetik kuvvet, parçacığın yükü (q), hız büyüklüğü (sürati) (|v|) ve o noktadaki manyetik alan şiddeti (|B|) ile doğru orantılıdır. Ayrıca parçacığın o noktadan geçerken sahip olduğu hız vektörü ile o noktadaki manyetik alan vektörü arasındaki açıya da bağlıdır. Yönü ise o noktadaki manyetik alan vektörüne ve o noktadan geçerken parçacığın sahip olduğu hız vektörüne diktir. Manyetik kuvvet, şu genelleştirilmiş ifade ile hesaplanır: F=qvXB.
Dolayısıyla, metal çubuğun içinde gezebilir durumdaki elektronlar, bir manyetik kuvvete maruz kalacaklardır. Elektronlar çubuğun içinde oradan oraya çarpıp sekerek hareket ederler, hız vektörleri sürekli değişir. Ancak, çubuk ile birlikte ötelenir durumda oldukları için, elektronlara etki eden manyetik kuvvetin baskın kısmı bu ötelenme hızından gelir. Bu şekilde elektronlar çubuğun 2 numaralı ucuna doğru kümelenmeye başlar, 1 numaralı uca doğru da bir pozitif yük fazlası kalır. Ancak çubuk içindeki yük dağılımının homojenliği bozulduğundan, bir elektrik alan da indüklenmiş olur. Bu elektrik alan da elektronlara bir kuvvet uygular, ancak bu kuvvet manyetik kuvvete göre ters yöndedir. Dolayısıyla, (hızlı bir şekilde) bir dengeye ulaşılır. Denge durumunda çubuğun iki ucu arasında bir potansiyel farkı oluşmuştur! Gerçekten de, çubuğun iki ucunu bir voltmetrenin uçlarına bağladığınızda bu potansiyel farkını ölçebilirsiniz.
Manyetik kuvvet ile ilgili en ilginç nokta, etki ettiği cismin hızı ile orantılı olmasıdır. Bir cismin hızı, farklı eylemsiz gözlemcilere farklı görünür. Dolayısıyla, farklı eylemsiz gözlemciler, aynı cisim için farklı manyetik kuvvetler ölçer. Ancak bu ciddi bir durumdur: Galileo’cu görelilik ilkesine göre, bir cismin üzerine etki eden kuvvetlerin tüm eylemsiz gözlemcilere aynı görünmesi gerekiyordu. Zira (hayali kuvvet olmayan) her kuvvetin, varlığını gözlemcilerden bağımsız olarak gösterebileceğimiz bir maddi kaynağı olmalıydı. Bu örnekte maddi kaynak, manyetik alandır. Peki, nasıl olur da, bir kuvvet kaynağı, eylemsiz gözlemcilerin farklı göreceği türden bir kuvvet oluşturur?
Durumun ilginçliğini biraz daha vurgulamak için, iki tane spesifik eylemsiz gözlemciyi ele alabiliriz. Örneğimizi laboratuvarda gerçekleştirdiğimiz bir deney olarak ele alırsak, bir gözlemci laboratuvarda oturan deneyci, diğer eylemsiz gözlemci de çubuğun kendisi olabilir. Çubuğun referans sisteminden bakıldığında, (bir manyetik alanın varlığına dair deneyciden çubuğa bilgi verilmediği sürece) çubuk bir manyetik alanın var olduğunu düşünmeyecektir, zira kendisini ve dolayısıyla üzerindeki yükleri (büyük ölçekten bakıldığında) durgun görmektedir. Ama uçları arasında bir potansiyel farkı vardır. Gerçekten de, çubukla aynı hızda hareket eden bir voltmetreyle ölçüm yaparsanız, bu potansiyel farkını yine görürsünüz (bunu evde deneyebilirsiniz). Bu durumda çubuk, dışarıdan kendisine paralel bir elektrik alanın uygulandığını düşünecektir. Dışarıdan uygulanan elektrik alan zıt yükleri zıt yönlere ittirmiş, dolayısıyla yükler de bir tepki elektrik alanı oluşturmuş ve dengeye gelmiştir.
Peki ama, laboratuvarda oturan deneyci çubuğa elektrik alan uygulamadığı ve fakat manyetik alan uyguladığı halde, çubuk neden manyetik alanı görmeyip de “olmayan” bir elektrik alanı görmektedir? Buradaki ilk yanıt şudur: Elektrik ve manyetik alanlar aslında aynı olgunun farklı görünüş biçimleri olmalılar. Buraya kadar tamam, ancak şöyle bir sorun var: Eylemsiz gözlemciler, kuvvet kaynaklarını gözlemciden bağımsız olarak aynı şekilde görmeliler ve burada bir gözlemci yalnızca çubuğa dik yönlü manyetik alan vektörleri görürken, diğer gözlemci çubuğa paralel yönlü elektrik alan vektörleri görmektedir. Gözlemciler aynı kuvveti gördükleri halde aynı maddi kaynağı görememektedir ve bu durum Galileo’cu koordinat dönüşümleri açısından olanaksızdır.[19] Elbette şu soru sorulabilir: Elektrik ve manyetik alanlar aynı olgunun farklı görünümleriyse, neden aynı maddi kaynak görülüyor olmasın? Teknik ayrıntılara giremeyecek olmakla birlikte şunu ifade etmemiz gerekir ki, söz konusu deneysel koşullar farklı türde kaynaklarla üretilmektedir. Deneycinin örnekte gösterilen türde bir manyetik alan görmesi için deney düzeneğinin etrafında belirli bir akım konfigürasyonunun oluşturulması veya uygun mıknatıslar kullanılması gerekir; düzenekteki yükler ise (çubuğun üzerindekiler değil) uzaya homojen dağılmış durumda olacaktır (yani her noktada net yük sıfır olacaktır). Ama çubuğun gördüğü elektrik alanı (indüklenen değil, “dışarıdan uygulanan”) oluşturmak için, çubuğun iki tarafında uygun şekilde statik yük konfigürasyonları oluşturmak gerekir; düzenekteki yükler uzaya homojen dağılmamış olmalıdır. Daha net bir açıklama için, matematiğe başvurmaktan başka çare olmadığından, burada durmak zorundayız. Yine de durumun yeterince açıklanabildiğini umuyoruz.
Bu noktada şöyle bir soru ortaya çıkar: O zaman, hareket durumu mutlak olan bir eylemsiz gözlemci varsayıp, tüm cisimlerin hareket durumlarını ona göre mi tarif etmeliyiz? Bu görüş, “Esir” kavramı ile tarif edilen bir ortamın olduğu varsayılarak tarif edildi (Giancoli, 2008: 954), ancak Galileo’cu görelilik ilkesini kurtaramadı. Belki Galileo’cu görelilik ilkesinden vazgeçilmeliydi, ama böyle bir tutumu gerekçelendirecek ampirik veriye gereksinim vardı. Michelson ve Morley’in ünlü deneyi, ihtiyaç duyulan ampirik veriyi sağlamayı umdukları halde bunun imkansızlığını ortaya koydu (Rindler, 2006: 9).
2.1.2 Michelson - Morley deneyi
Deney, basit bir fikre dayanıyordu (Rindler, 2006: 9-10): Eğer hareket durumu mutlak olarak kabul edilebilecek bir ortam, bu örnekte “Esir”, varsa ve ışık bu ortamda taşınan dalgalardan oluşuyorsa (bu ikinci varsayım ışığın niteliği ile ilgili, burada ayrıntılandırmayacağız), Dünya’nın Esir’e göre hızı ile aynı yönde hareket eden ışık dalgalarının hızı, başka yönlerde hareket eden ışık dalgalarının hızından farklı olarak ölçülmelidir. Aşağıdaki şekilde Michelson İnterferometresi adı verilen bir düzenekte bu amaçla ölçüm yapılabilir. Aynı kaynaktan çıkan ışık ışınlarını ikiye bölüp, iki ışını farklı uzunlukta optik yollardan geçirerek aynı ekrana düşürdüğünüzde, optik yol farkından kaynaklanan bir girişim deseni görmeyi beklersiniz. Michelson İnterferometresi bu işe yarar.
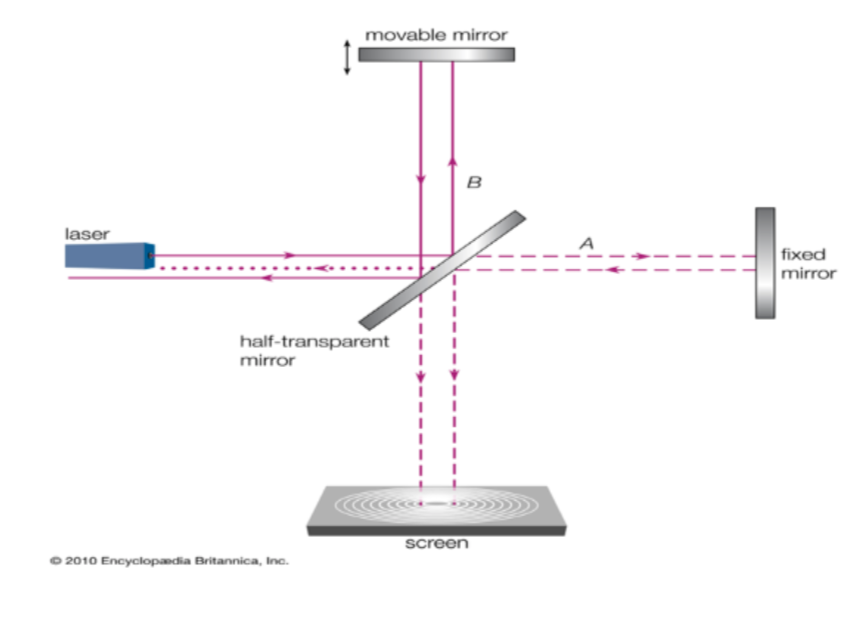
Işığın boşluktaki hızının gözlemciden bağımsız bir evrensel sabit olması, önemli sonuçları olan bir bulguydu. Bu sonuçlardan biri, evrende hareket durumu mutlak addedilebilecek bir ortamın (Esir; bkz. Rindler, 2006: 9) var olduğunu düşünmenin gereksiz olduğu ve böyle bir ortamın var olmadığını basitçe varsayabileceğimiz sonucuydu. Diğer sonuçlar ise, hareket olgusunu kavrayışımızda önemli etkiler yarattı.
2.1.3 Özel görelilik kuramı
Einstein, ünlü 1905 makalelerinden biri olan “Yüklü cisimlerin elektrodinamiği üzerine” başlıklı çalışmasında (Einstein, 1990), bu ilginç bulguyu bir postüla olarak kabul eden yeni bir yaklaşım ortaya koydu (Rindler, 2006: 12). Yaklaşımın diğer postülası ise, fizik yasalarının tüm eylemsiz gözlemciler için aynı şekilde ifade edilebilmesi gerektiğiydi (Rindler, 2006: 12). Şimdilik “Einstein’cı görelilik ilkesi” olarak anacağımız bu yaklaşım, kabul edilmesi ilk anda zor gelen çeşitli mantıksal sonuçları da çağırıyordu. Bunlardan iki tanesi özellikle aydınlatıcıdır.
Mantıksal sonuçlardan biri, zaman ve uzam aralıklarının farklı eylemsiz gözlemciler tarafından farklı ölçülebileceği sonucudur. Bu durumu yine klasikleşmiş bir örnekle açıklayabiliriz.[21]
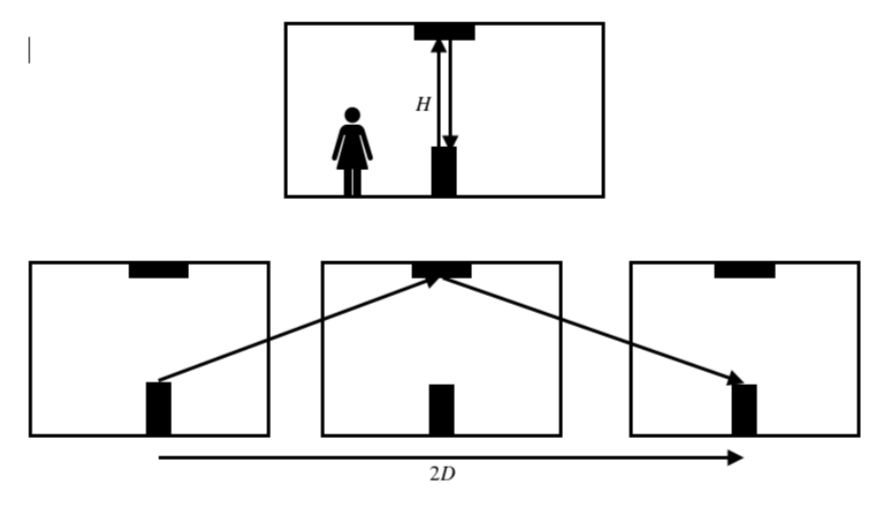
Farz edelim ki, Uluslararası Uzay İstasyonu’nda bir göreve katıldınız. Görevde sizden bir deney yapmanız istendi. Uzay İstasyonu’nda bulunduğunuz bölmede Dünya’ya en yakın noktaya bir lazer koyup Dünya ile istasyonu birleştiren doğruyla hizalamanız gerekiyor. Lazerin tam karşısında aynı doğru üzerinde ve Dünya’dan öteye bakan bir noktaya da bir ayna koymanız gerekiyor. Ayna ile lazer arasındaki uzaklığı H olacak şekilde ayarlıyorsunuz. Lazerden bir ışık ışını gönderip, aynadan yansıması ve lazere geri dönmesi için geçen süreyi ölçüyorsunuz. Bu şekilde ışığın hızını hesaplamış oluyorsunuz. Bu süreci Dünya üzerinde gözlemleyen başka bir gözlemci daha var ve deney sonunda iki gözlemcinin ışık hızı ölçümleri karşılaştırılıyor.
Deney esnasında Uzay İstasyonu da Dünya’ya göre hareket halinde olduğundan, ışık ışınının lazer -ayna - lazer rotasında kat ettiği yollar istasyonda ve Dünya’da bulunan gözlemcilere göre farklıdır. Deney küçük bir mesafede gerçekleşirken istasyon da büyükçe bir çember yayı çizmeyeceğinden, istasyonun deney süresince yaklaşık olarak düz bir çizgide hareket ettiğini varsayabiliriz. Bu süreçte yerdeki gözlemci istasyonun toplamda 2D kadar yol kat ettiğini ve u hızıyla hareket ettiğini ölçmüş olsun. Dolayısıyla, Şekil 3’te görülen durum ortaya çıkmış olur.
İstasyondaki gözlemciye göre ışık ışını 2H kadar yol kat etmiştir. Bu yolu Δt1 kadar sürede kat ettiyse, hızı \(c_1=2H/Δt_1\) olarak ölçülür. Yerdeki gözlemciye göre ise ışık ışını 2\(\sqrt{H^2+D^2}\) kadar yol kat etmiştir. Bunu Δt2 kadar sürede kat ettiyse, hızı \(c_2=\frac{2\sqrt{H^2+D^2}}{Δt_2}\)olarak ölçülür. Michelson-Morley deneyinin bize gösterdiği üzere \(c_1=c_2=c\) olması gerektiğini dikkate alırsak, şu sonuca varırız: \((cΔt_1)^2-4H^2=(cΔt_2 )^2-4(H^2+D^2)\).
Deneye dair başka bir bilgi de şudur: Deney süresince istasyon u hızıyla hareket ederek toplamda 2D kadar yol kat etmiş olduğuna göre, \(2D=uΔt_2\) olur. Dolayısıyla, \(4D^2=(uΔt_2)^2\) olur. Bunu bir önceki sonucumuzla birleştirirsek, \((cΔt_1)^2-4H^2=(cΔt_2)^2-4H_2 -(uΔt_2 )^2\) olur. Bu da demektir ki, \(c^2 Δt_1^2=(c^2 - u^2 )Δt_2^2\), yani: \(\frac{Δt_2}{Δt_1}=\frac{1}{\sqrt{1-u^2/c^2}}\). Demek ki, gözlemcilerimiz deneyin gerçekleştiği zaman aralıklarını farklı ölçtüler.
Burada görülen olguya “zaman genişlemesi” adı verilir (Giancoli, 2008: 960). Bunun muadili olarak, gözlemcilerimiz uzunlukları da farklı ölçerler. Yukarıdaki örnekte bu bilgiyi kullanmamış olmamızın sebebi, göreli hareket doğrultusundaki uzunluklar farklı ölçüldüğü halde göreli hareket doğrultusuna dik doğrultulardaki uzunlukların aynı ölçülmesidir (detaylar için bkz. Giancoli, 2008: 964-965). Çıkarsamasını okura bırakarak şu bilgiyi not edelim: Uzay İstasyonu’nda bulunan ve Uzay İstasyonu’nun yere göre hareketiyle aynı doğrultuda uzanmış rijit bir çubuğun uzunluğu istasyonda L olarak ölçülüyorsa, yerdeki gözlemci aynı çubuğun uzunluğunu \(L\sqrt{1-u^2/c^2}\) olarak ölçecektir (Giancoli, 2008: 964-965). Kareköklü faktörün 1’den küçük olduğu göz önüne alınırsa, yerdeki gözlemcinin istasyondaki gözlemciye göre daha küçük bir uzunluk ölçeceğini anlarız, buna “uzunluk büzüşmesi” (length contraction) denir (Giancoli, 2008: 964-965). Önemli olan nokta şudur: Uzamsal ve zamansal aralıkların bir eylemsiz gözlemciden diğerine değişmeyen nicelikler olması fikri terk edilmek zorundadır. Ancak yine de bir eylemsiz gözlemciden diğerine değişmeyen bir nicelik vardır: Uzay-zaman aralığı. Yukarıdaki örnekte, gözlemcilerin ölçtüğü uzay-zaman aralıkları şöyleydi: \((cΔt_1)^2-4H^2=(cΔt_2 )^2-4(H^2+D^2)\).
Bu ne demek? Uzayımız halen üç boyutlu değil mi? Zaman farklı bir anlam mı kazandı?
Uzay ve zamanın anlamlarının birbirine karıştığı açıktır. Uzay ve zaman kavramlarımızın, birbirine denk olarak ele alındığı bir kavrayışa geçmemiz gerekir. Peki bu durum, gerçeklik algımızın, veya nesnelliğin gözlemciden gözlemciye değişen bir niteliği olduğunu mu açığa çıkarır?
Şüphe yok ki, böylesi bir çıkarım saçmadır. Galileo’cu ve Einstein’cı görelilik ilkeleri arasındaki temel fark, eylemsiz gözlemcilerin hangi fiziksel nicelikleri aynı göreceğine dair bir hipotez farkıdır. Elbette bu fark önemsiz değildir. Ancak, gözlemciden gözlemciye değişen bir gerçeklik fikrine başvurulmadığı açıktır; gerçeklik, “olaylarla” (ışının lazerden çıkması, aynaya çarpması, lazere dönmesi ve benzeri) ifadesini bulur. Bir olay geçekleştiyse, tüm gözlemcilere göre gerçekleşmiştir. Dahası, iki ilke arasında bir ilişki de vardır. Bunu en kolay şekilde açıklamanın yolu, yukarıdaki örneği takip etmek olacaktır.
Şüphe yok ki, böylesi bir çıkarım saçmadır. Galileo’cu ve Einstein’cı görelilik ilkeleri arasındaki temel fark, eylemsiz gözlemcilerin hangi fiziksel nicelikleri aynı göreceğine dair bir hipotez farkıdır. Elbette bu fark önemsiz değildir. Ancak, gözlemciden gözlemciye değişen bir gerçeklik fikrine başvurulmadığı açıktır; gerçeklik, “olaylarla” (ışının lazerden çıkması, aynaya çarpması, lazere dönmesi ve benzeri) ifadesini bulur. Bir olay geçekleştiyse, tüm gözlemcilere göre gerçekleşmiştir. Dahası, iki ilke arasında bir ilişki de vardır. Bunu en kolay şekilde açıklamanın yolu, yukarıdaki örneği takip etmek olacaktır.
Gözlemcilerimizin zaman aralığı ölçümlerinin farklı olması gerektiği sonucunu çıkarmıştık: \(\frac{(Δt_2)}{(Δt_1)}=\frac{1}{\sqrt{1-u^2/c^2}}\). Şimdi, Uzay İstasyonu’nun hızının ışık hızına kıyasla ihmal edilebilir bir değere sahip olduğu koşulları düşünelim. Bu durumda, u2/c2 terimi 1’e kıyasla çok küçük olacaktır. Bu terimi ihmal edebileceğimiz rejimde, \(\frac{(Δt_2)}{(Δt_1)}=1\) olur: Yani, gözlemcilerimiz zaman aralıklarını aynı ölçer. Benzer bir durumu uzamsal aralıklar için de göstermek mümkündür. Biraz daha ilerleyince, şu sonuca varırız: Galileo’cu görelilik ilkesi, Einstein’cı görelilik ilkesinin (ışık hızına kıyasla) küçük hızlardaki limitidir.[22]
Bu sonuç, çokça karşımıza çıkan genel bir sonuçtur. Modern fizikte her yeni kuram, belirli spesifik rejimlerdeki limitlerinde[23] eski kuramlara denk olmak zorundadır. Bunu bir epistemolojik standart olarak kabul etmiş bulunuyoruz. Bu standart, tarih yazımında genellikle Galileo-Newton çizgisiyle başladığı kabul edilen bilim geleneğinin içsel mantığının diyalektik bir işleyişe sahip olmak zorunda olduğunun başat göstergesidir.
Burada, olası bir yanlış anlamanın önüne geçmek faydalı olacaktır. Einstein’cı ve Galileo’cu görelilik ilkeleri arasında nicel bir ilişki tarif edilebilmesi, Einstein’ın görelilik ilkesini Galileo’nun görelilik ilkesinin bir genellemesi olarak okumak şeklinde bir yorumu davet edebilir. Einstein’ın görelilik ilkesinin daha “genel” olduğu doğrudur; yani Galileo’nun görelilik ilkesinin yaklaşık olarak bile işlemeyeceği durumlarda işleyebilir. Ancak, Einstein ilkesi, Galileo ilkesinin bir genellemesi değildir. Genellemeler, hali hazırda birbiriyle tutarlı olan ancak farklı şekillerde ifade edilmiş önermelerin ortaklaştırılmasıdır. Galileo ve Einstein ilkeleri arasında ise apaçık bir çelişki vardır. Felsefi temelleri ve sonuçları arasında ortaklıklar olduğu kadar farklar da mevcuttur. Yukarıdaki örneğimizde açıkça görüldüğü üzere de, birbiriyle çelişen öngörüler yapmaktadırlar. Peki, bu durum, düşük hız limitinde Einstein ilkesinden Galileo ilkesine geçilebildiği iddiasıyla çelişiyor mu?
Tabii ki çelişmiyor. İki ilke arasında kurduğumuz ilişki, birinin kesin (exact) öngörüsünün, belirli koşullar altında, diğerinin yaklaşık (approximate) öngörüsü olmasıdır. Burada, Galileo ilkesinin kesin öngörüsü, Uzay İstasyonu yeterince yavaş hareket ediyorsa, Einstein ilkesinin yaklaşık öngörüsüne eşittir. Örneğin, Einstein ilkesini temel alan bir analizde (hesabı kolaylaştırmak ve benzeri sebeplerle) yaklaşık olarak Galileo ilkesine başvurulması, Galileo ilkesinin felsefi temellerinin esas alındığı anlamına gelmemektedir. Tam aksine, Einstein ilkesinin felsefi temelleri esas alınıyor demektir. Böyle olmasa, örneğin Newton’un hareket kuramına başvurularak icra edilen hiçbir mühendislik disiplini gelişemezdi.
Peki, iki ilke arasındaki ilişkiyi nasıl tarif etmeliyiz? Burada tercih edeceğimiz yaklaşım, “içerme - aşma ilişkisi” yaklaşımıdır. Einstein ilkesi, Galileo ilkesini aşmıştır; zira onun çelişkiye düştüğü kimi durumları açıklamayı başarmıştır ve onun öngöremeyeceği ve deneylerle doğrulanabilen yeni olgular öngörebilmektedir. Aynı zamanda Einstein ilkesi Galileo ilkesini içermektedir; Galileo ilkesinin felsefi temellerinin bir kısmı (örneğin eylemsizlik ve eylemsiz gözlemci kavramları) ve nicel öngörüleri Einstein ilkesi tarafından yeniden üretilebilmektedir. Yukarıda bahsi geçen epistemolojik standart bunu gerektirmektedir.
Bu bölümün en başında, Einstein’cı görelilik ilkesinin mantıksal sonuçlarından iki tanesinin özellikle aydınlatıcı olduğunu söylemiştik. Bunlardan biri yukarıda sunuldu. Şimdi diğerini inceleyebiliriz.
Diğer mantıksal sonuç, “eşzamanlılığın göreliliği” olgusudur. Herhalde Einstein’cı görelilik anlayışının en popüler ve sağduyuyu zorlayan sonuçlarından biri budur. Bu olguyu izah etmek için yine bir düşünce deneyine başvurabiliriz (benzer bir örnek için Rindler, 2006: 38-39).
Yere göre sabit bir v süratiyle belirli bir yönde düz bir çizgi üzerinde ilerleyen bir tren düşünelim. Trenin kendi referans sisteminde (yani durgun göründüğü sistemde) ölçülen toplam uzunluğu \(2L\) olsun. Trenin tam orta noktasında bir ışık kaynağı, iki ucunda da birer dedektör olsun. Her zamanki gibi, biri trende biri yerde bulunan iki eylemsiz gözlemcimiz olsun. Trenin ortasındaki kaynaktan trendeki gözlemciye göre eş zamanlı olarak iki ışık ışını trenin her iki ucuna doğru gönderilsin. Trendeki gözlemci, iki ışının da uçlardaki dedektörlere aynı anda çarptığını görecektir. Peki, yerdeki gözlemci bu olayları hangi sırayla görecektir?
Gündelik hayat tecrübemiz, nesnelerin hızlarını toplayıp çıkararak göreli hızlarını hesaplamamızı söyler; bu yaklaşım aslında Galileo’cu görelilik ilkesine de uygundur. Yerdeki gözlemcinin de trenin hareket yönünde ve tersi yönde hareket eden ışık ışınlarının hızlarını buna göre ölçeceğini, dolasıyla ışınların yerdeki gözlemciye göre dedektörlere aynı anda ulaşacağını düşünürüz. Yani, yerdeki gözlemciye göre trenin önüne doğru ilerleyen ışının sürati \(c+v\), arkasına doğru ilerleyen ışının hızı da \(c-v\) olmalıdır. Bu nedenle, ışınlar da trenle birlikte sürüklenmiş olur ve dedektörlere ulaşma süreleri yalnızca trenin uzunluğuyla ilgilidir.
Ama Einstein’cı görelilik ilkesi, Michelson-Morley deneyinin işaret ettiği bir bulguyu esas alıyordu. Buna göre, her iki gözlemci de ışık ışınlarının hızını c olarak ölçmeliydi. Yani \(c±v\) gibi bir ölçüm yapılması mümkün değildi. Bu durumda, yerdeki gözlemci için olaylar silsilesi farklı olacaktır. Yerdeki gözlemciye göre trenin arkasına doğru ilerleyen ışık ışını \(ΔT_1\) kadar sürede, trenin önüne doğru ilerleyen ışın da \(ΔT_2\) kadar dedektöre ulaşmış olsun. Aynı olaylar trendeki gözlemciye göre sırasıyla \(Δt_1\) ve \(Δt_2\) sürede gerçekleşmiş olsun. Trendeki gözlemci trenle birlikte hareket ettiği için \(Δt_1=Δt_2≡Δt=\frac{2L}{c}\) olur. Ama yerdeki gözlemci bu zaman aralıklarını (ve trenin uzunluğunu) farklı ölçecektir. Işın ile trenin arkasındaki dedektör birbirine doğru hareket ettiği ve ışın yerdeki gözlemciye göre de c süratiyle hareket ettiği için, \(ΔT_1<Δt\) olur. Benzer şekilde, trenin önündeki dedektör ile ışın aynı yönde hareket ettikleri için, ışının ön taraftaki dedektöre ulaşması trendeki gözlemcinin gördüğünden daha fazla zaman alır, \(ΔT_2>Δt\) olur. \(ΔT_1\) ve \(ΔT_2\) sayılarının hesabını ilgili okurların merakına bırakarak, sonucu ifade edelim: “Eşzamanlılık” olgusu görelidir; bir gözlemciye göre eşzamanlı gerçekleşen olaylar, başka bir gözlemciye göre eşzamanlı olmayabilir. Olayların “gerçekte” eş zamanlı olup olmadığı sorusu yanlıştır; her iki yorum da aynı derecede gerçekliği tarif eder. Böyle bir düşünceyi tam olarak kavrayabilmek için, uzamsal ve zamansal aralıkların birbirinden bağımsız olarak her eylemsiz gözlemci için aynı olması gerektiği varsayımından vazgeçmiş olmak gerekir.
Ancak daha ilginç olan bir konu vardır. Eşzamanlılığın göreliliği olgusu, akıllara şöyle bir soru getirir: Bir gözlemci \(A\) ve \(B\) gibi iki olayı “önce \(A\), sonra \(B\)” sırasıyla görmüş olsun. Başka bir gözlemci aynı olayları “önce \(B\), sonra \(A\)” sırasıyla görebilir mi? Sorunun yanıtı şöyledir: Eğer A ve B olayları birbirine nedensel olarak bağlıysa, yani A olayından u hızıyla (\(u≤c\) olmak üzere) yayılan bir enformasyonun B olayına ulaşması mümkün ise, hayır (Rindler, 2006: 56). Buradaki kritik unsur, “enformasyon”dur. Özel görelilik kuramına göre, enformasyon taşıyan her tür sinyalin hızı, ışığın boşluktaki hızı ile sınırlandırılmıştır. Özel görelilik, kuramı, olaylar arasındaki nedensellik ilişkilerinin koruduğunu varsayar. Dolayısıyla, özel göreliliğin temel varsayımlarını, “görelilik ilkesi” ve “nedenselliğin korunması ilkesi” olarak ifade edebiliriz (Rindler, 2006: 15, 56).
Dikkatli bir gözün fark edeceği üzere, şu ana kadar, nesnel gerçeklik kavrayışından herhangi bir taviz verilmemiştir. Fiziksel olayların nesnelliği, görelilik anlayışının temeli olmaya devam etmektedir. Ayrıca, fiziksel olayların “enformasyonunun” yine fiziksel bir olgu olduğu, fizik yasalarına tabi olduğu anlayışı devreye girmiştir. Newton’cu hareket kuramında cisimlerin birbirleri arasındaki etkileşimin “anlık” olarak, yani hiç vakit harcamaksızın iletilebilir olması, Newton’un kendisi için dahi felsefi açıdan sıkıntı veren bir konu iken, Einstein bunun zaten mümkün kabul edilmediği bir fizik yaklaşımı geliştirmiştir.
Enformasyonun maddi gerçekliğin bir parçası olarak ele alındığı ilk nokta muhtemelen 1905 yılı değildir. Ancak, bu anlayışın mantıksal sonuçları görelilik kuramına ilişkin tartışmaların da ötesine geçmektedir. Burada ayrıntılı olarak ele alamayacağımız bu konunun içeriğine dair fikir vermek için şunu söylemekle yetinelim: Fiziksel sistemler arasındaki etkileşim türlerinden bazıları, sistemlere dair enformasyon alış verişi amacıyla kullanılır. Dolayısıyla, bilinçli bir öznenin doğanın kendisinden edindiği enformasyon ile, bilince sahip olmayan iki nesne arasındaki etkileşim (kuvvet iletimi vb) olgusu arasında kategorik bir fark olmamalıdır. Einstein’cı görelilik ilkesinin temel varsayımlarından olan “nedenselliğin korunması” ilkesi bizi tek başına bu sonuca götürmüyor elbette. Ancak bu yaklaşımı kuvvetle desteklediğini iddia etmekte bir sakınca bulunmuyor. Daha da ilginci, Einstein'ın kendisini de felsefi açıdan ziyadesiyle rahatsız eden kuantum mekaniğinin, enformasyon olgusuna dair aynı yaklaşımı desteklediğini iddia etmek de mümkündür.[24] Bir kez daha ilgiyle görürüz ki, fizik bilimi “çelişkilerle” ilerlemektedir.
2.2 Genel görelilik kuramı veya göreliliğin genel kuramı
Bu noktaya kadar pek çok ilginç sorun tartışıldı. Ancak bir tanesi açık kaldı: Eylemsiz gözlemcileri tarif etmeye çalışırken kaçınamadığımız “mutlak arkaplan”, ya da başka bir deyişle tüm uzayı ve zamanı kaplayan düz koordinat sistemleri varsayımından nasıl kurtulacağız?
Bu sorun, Newton’un hareket kuramını değerlendirirken değindiğimiz başka bir konuyla ilgilidir: Kütleçekimi. Görelilik kavramı üzerine yapılan tarihsel yolculuğun başlangıç noktası, Kopernik’in evren modeli idi. Güneş merkezli evren modeli ile görelilik ilkesi arasındaki bağı kurarken, Newton’un kütleçekim yasasına başvurulmuştu. Ancak daha sonra kütleçekiminden bahsedilmedi.
Özel görelilik, Newton’un hareket kuramı gibi, bir tür “mutlak arkaplan” varsaymak durumundadır. Uzam ve zaman aralıklarının gözlemciden gözlemciye değişkenlik gösterdiği anlaşılmış olsa da, “üzerine etki edilemeyen düz bir uzay-zaman” gereksinimi geçerli kalmıştır. Özel görelilik bağlamında bunun karşılığı, arkaplan olarak bir Minkovskiyen uzay-zamanın varsayılmasıdır (Rindler, 2006: 35). Burada söz ettiğimiz unsur, kuramın temel varsayımlarından olmasa da, bir mantıksal zorunluluktur. Uzay-zamanın kendisi, maddenin varlığından bağımsız olarak varsayılmakta, madde onu etkileyememektedir. Peki, bu durumun kütleçekimi ile ilişkisi nedir? Esasen, kütleçekimi veya başka bir kuvvet maddenin uzay-zamanla etkileşmesi için olanak sağladığında, uzay-zamanın bir arkaplan olarak varsayılması gereği ortadan kalkardı. 20. yüzyılın başında elektromanyetik kuvvet ve Newton'un tarif ettiği haliyle kütleçekim kuvveti, belirli bir arkaplan uzayında tanımlanabilen ve incelenebilen kuvvetlerdi. Ama ikisinin tabi olduğu görelilik ilkeleri farklıydı ve ikisi de maddenin uzay-zamanla etkileşmesini ifade edecek bir unsur barındırmıyordu. Einstein, bu unsurun kütleçekimi ile ilgili olabileceğini fark etti (Rindler, 2006: 22).
Boş uzayda belirli bir ivmeyle düz bir çizgide hareket eden ve kendi ekseni etrafında da dönmeyen bir roket düşünelim (Rindler, 2006: 18). Roketin tabanında bir gözlemci duruyor olsun. Gözlemci, roketle birlikte ivmelenmektedir. İvmeye neden olan kuvvet, roketin tabanı tarafından gözlemciye aktarılmaktadır. Eğer gözlemci boş uzayda (yani potansiyel kuvvet kaynaklarından uzakta) ivmelendiği bilgisine sahip değilse, hissettiği kuvveti aynı ivmeyi sağlayan bir “ağırlıktan” ayırt edemeyecektir. Bu durum, “zayıf eşdeğerlik ilkesi olarak” da bilinen ve kütleçekim kuvvetinin ilginç bir özelliğini yansıtan bir durumdur (Rindler, 2006: 17). Bir kütleçekim alanında herhangi bir noktadaki alan değeri g ise, o noktaya koyulan herhangi bir cisme etki eden kuvvet mg kadar olur. Cisme etki eden başka bir kuvvet olmadığında, Newton'un ikinci yasasını kullanarak cismin ivmesini hesaplamak istersek \(\frac{mg}{m}=g\) buluruz. Bu nedenle de \(g\)’yi genelde “yer çekimi ivmesi” olarak anarız.
“Başka ne olabilirdi” diyebilirsiniz. Ama dikkatli okur, daha önceki kısımlarda “eylemsizlik kütlesi” şeklinde bir kavram kullandığımızı hatırlayacaktır. Bu kavram, “hareket durumunun değişimine gösterilen direnç miktarı” olarak yorumlanır ve Newton’un ikinci yasasında anılan kütledir. Bir de “gravitasyonel kütle” kavramı vardır; Newton’un kütleçekim yasasında anılan kütle değeridir. Örneğin Dünya üzerinde duran m kütleli bir cisme etki eden kütleçekim kuvveti \(\frac{GmM}{R^2}\) kadardır; burada G Newton sabiti, \(M\) ve \(R\) ise Dünya’nın kütlesi ve yarıçapıdır. Bu iki yasa, birbirlerinden bağımsız olarak tanımlanmıştır. Dolayısıyla, bir cismin “hareket durumunun değişimine gösterdiği direnç” olan eylemsizlik kütlesi ile “kütleçekim alanına verdiği tepkinin” miktarı olan gravitasyonel kütlesi birbirine eşit olmak zorunda değildir (Rindler, 2006: 16-18). Sağduyumuz, ve bugüne kadar bidiğimiz fizik biliminin ampirik başarıları bu iki niceliği birbirine eşit kabul etmenin gayet makul olduğunu söyler. Ancak sağduyu fizik bilimi için yeterli değildir: Bu iki niceliğin birbirine oranı, Galileo’dan başlayarak, andığımız ve anmadığımız çokça bilim insanı tarafından deneysel olarak ölçülmektedir. Ölçümler 1012’de 1 mertebesine kadar hassaslaşmıştır (Rindler, 2006: 17)[25] , ve iki niceliğin eşit olduğunu söylemektedir. Tam olarak bu nedenle, kütleçekim alanının cisme sağladığı ivmenin değeri, cismin kütlesinden bağımsız olur.
Roketteki gözlemcimize dönersek, şunu fark ederiz: Bu gözlemci için, hissettiği kuvvetin söyleyeceği değerde bir ivme ile, aynı değere sahip bir kütleçekim alanı arasında hiçbir fark yoktur. Dolayısıyla, örneğin belirli bir kütleçekim alanında serbest düşme halindeki bir gözlemciyi referans aldığımızda, kendisini ve kendisiyle birlikte serbest düşme halindeki tüm diğer cisimleri de eylemsiz olarak görür. Uluslararası Uzay İstasyonu’ndaki bilim insanları tam olarak bunu deneyimlemektedir. Bir anlamda, kütleçekim kuvveti ile Newton’un ikinci yasası arasındaki ilişkinin, diğer kuvvetlerin ikinci yasa ile ilişkisine kıyasla daha özel olduğunu söyleyebiliriz.
Einstein'ın fark ettiği durum işte buydu. Kütleçekimi, uygun bir koordinat dönüşümü bulunarak elimine edilebiliyordu (Rindler, 2006: 18). Dolayısıyla, serbest düşme halindeki cisimlerin de eylemsiz gözlemci olarak kabul edilebilmesi gerekirdi. Ancak serbest düşme halindeki gözlemciler, sonuçta, Newton’cu paradigmaya göre ivmeli gözlemci idi. Dolayısıyla, serbest düşme halindeki bir gözlemcinin eylemsiz gözlemci gibi değerlendirilmesi nasıl mümkün olacaktı?
Newton’cu paradigma içinde bu mümkün değildir. Teknik ayrıntılarına girmeden şu bilgiyi vermekle yetineceğiz: Serbest düşme halindeki gözlemciler “yerel olarak eylemsiz” olarak değerlendirilir ve boş uzayda tüm kuvvet kaynaklarından uzaktaki cisimlerden farksızdırlar. Bu farksızlığı anlamanın ve ifade etmenin tek yolu ise, uzay-zaman geometrisinin nasıl olduğuna dair bir ön varsayım yapmamaktan geçer. Newton’un ve özel göreliliğin tüm uzay-zamana (an azından sonlu büyüklükte parçalarına) yayılabilen eylemsiz koordinat sistemleri terk edilmek zorundadır. Maddenin uzay-zaman içindeki dağılımı ile etkileşen dinamik bir geometride, serbest düşme halindeki cisimler yerel olarak eylemsizdir ve yerel olarak eylemsiz olan tüm gözlemciler birbirine denktir. Daha kuuvetli bir argüman ise şudur: Yerel olarak eylemsiz olan gözlemcilerin ifade ettiği şekilde fizik kanunları tüm gözlemciler için aynı olmalıdır (Misner, 1973: 387). Uzay-zaman geometrisini önsel olarak belirlenen değil, maddenin evrimiyle birlikte evrilen dinamik bir yapı olarak ele almanın aracı olan Riemmann geometrisi, fizik yasalarını tüm gözlemcilerin aynı şekilde ifade edebilmelerini de sağlar. Uzay-zaman aralıkları ise halen gözlemciden gözlemciye değişmeyen niceliklerdir.
Daha fazla matematiğe başvurma zorunluluğu yaratmamak için, burada durabilir ve felsefi konularda görüş oluştururken hangi hususlara dikkat etmek gerektiğini tartışabiliriz.
3. Felsefi çıkarımlar nelere dikkat etmeli?
Bu noktaya kadar, hareketin göreliliği fikrinin tarihteki yerini, içeriğini ve tarih içinde nasıl evrildiğini örneklerle açıklamaya çalıştık. Elbette görelilik fikrine ve hareket kuramlarına dair tartışılacak başlıkların sayısı bu çalışmanın sınırlarını çokça aşacaktır. Yine de, bu çalışmanın amaçladığı bazı yöntemsel konular için yeterli materyal oluştuğunu düşünüyoruz.
“Yöntem” kavramı ile başlanabilir. Yine kendine ait genişçe bir literatüre sahip bir kavram için, tartışmamıza odaklı bazı sınırlar çizmemiz gerekmektedir.
Fizik biliminin bir yöntemi vardır. Basitleştirmek istersek bunu “düşünme biçimi” olarak da ifade edebiliriz. Okullarda ve hatta bilim insanlarının yetiştiği süreçlerde bu yöntem, usta çırak ilişkisi içinde ve pratikte öğrenilmektedir. Her zaman ve her örnekte doğru öğrenildiği elbette söylenemez, ancak fizik camiasının bilgi üretme pratiği incelendiğinde, özellikleri kendini gösteren bir “yöntem örüntüsü” görebildiğimizi iddia edebiliriz.
Bahsettiğimiz yöntem, “bilgiyi üretmenin yöntemidir” ve aslında fizik bilimine özgü değildir; veya fizik bilimine özgü olmak zorunda değildir. Dolayısıyla, fizik bilimi ve bu çalışmada yürüttüğümüz tartışma açısından önemli olan bazı özelliklerini ele almamız yeterli olacaktır.
Her şeyden önce, yöntemin tarihsel ve kolektif niteliğine vurgu yapmak gerekmektedir. Hiç bir ilke, yasa veya kuram, onu formüle eden bilim insanı veya insanlarının felsefi görüşlerinin birebir yansıması, çıktısı veya uzantısı değildir. Elbette bunlardan etkilenir, hatta bilim insanının üretim pratiği içinde aralarında doğrudan bir ilişki de kurulabilir. Ancak, fizik biliminin bir özelliği, fizikte kuramların, yasaların ve ilkelerin, onları ilk olarak veya güncelleyerek formüle eden bilim insanının dünya görüşünden bağımsızlaşabilmesidir. Bilim insanının öznelliğine hapsolan veya koşullar nedeniyle bilim insanının kendisi dışında kimsenin ilgi göstermediği kuramların gelişmesi pratik açıdan mümkün değildir, dolayısıyla içerik açısından da mümkün olmaz.
Yöntemin başka bir özelliği, fizik biliminin bilgi dağarcığını herhangi bir kuramla sınırlı tutmamasıdır. Galileo’dan Einstein’a kadar takip ettiğimiz akıl yürütmelerde, önce belirli bir kuramsal yapıyı kurmaya yarayan ama sonra eleştiriye tabi tutulan ve “aşılan” çeşitli unsurlar gördük. Bir de, vazgeçilmeyen unsurlar vardı: Görelilik fikrinin kendisi gibi. Dolayısıyla, görelilik fikrinin Galileo’dan günümüze öyküsünü incelediğimizde, uzun bir zaman ölçeğine yayılan kolektif bir aklın diyalektik muhakemesi olduğunu görürüz. Tarihin bir noktasında görelilik fikrinden vazgeçilmesinin de tartışıldığını gördük (Esir fikri ve Michelson-Morley deneyi örneğinde). Bilim tarihinde bunun başka örnekleri de vardır. Tabii, günün sonunda, görelilik fikrinden vazgeçilmedi. Ancak fikrin felsefi temelleri ve içeriği ciddi bir değişim geçirmiş oldu. Bugünün bilgi düzeyiyle şu soruyu sormak mümkündür: En baştan, Galileo’nun zamanında, bu içeriği öngörmek tamamen olanaksız mıydı?
Bu sorunun yanıtı “neredeyse olanaksızdı” olarak verilebilir. Çok çeşitli nedenler sıralanabilir ve bu nedenlerin arasında insanlığın o dönemde mevcut olan gelişmişlik düzeyi, kavram dağarcığı ve benzeri hususlara vurgu yapılacaktır. Bunlar arasında bazıları, fizik bilimi söz konusu olduğunda hemen kendini gösterir. Fizik kuramları, yasaları, ilkeleri, maddi gerçekliğin bütünlüğü içinde tasvir ve taklit edebildikleri parçalara odaklanır (kavram dağarcığı, teknolojik düzey, matematik bilgisinin düzeyi, çalışmaları etkileyen toplumsal koşullar burada devreye girer). Bunların soyut (matematiksel) temsillerini yaratır (“soyut makineler”) ve gerçekliğin geri kalanını zorunlu olarak budar. Bu budama işlemi, gerçekliğin geri kalanının önemsiz olduğu şeklinde bir felsefi yorumla ilişkilenebileceği gibi, “bilim çeşitli yaklaştırmalardan ibarettir” şeklinde özetleyebileceğimiz bir araçsalcılıkla da ilişkilenebilir. Ancak, yukarıda anlatmaya çalıştığımız öyküye bakıldığında, budama işleminin adım adım geri alındığı, gerçekliğin budanan parçalarının kuramsal yapılar içinde yeniden üretilmeye çalışıldığı görülecektir. Newton’un “noktasal parçacıklarından” cisimlerin “aslında noktasal olmadıkları ama noktasal bileşenlerden oluştukları” yaklaşımına geçiş bunun bir örneğidir. Bazen de budanmış dalları yeniden eklemek aynı kuramsal yapının içinde mümkün olmaz; bu noktada da, “var olan kuramı aşan” yeni bir kuramın kendini göstermesi tek çözümdür.
Görelilik fikrinin öyküsü, budanmış gerçekliğin soyut temsilinden maddi gerçekliğin bütünlüğüne ulaşma çabasını ve bu sürecin diyalektik işleyişini en berrak şekilde ortaya koyan örneklerden biridir. Bu öyküde, tarihin akışının davet ettiği bazı sıçramalar (örneğin Newton'un hareket kuramı, özel görelilik kuramı) görüldüğü gibi, bilim insanının bu süreçteki mantığı doğru kavrayıp devrimci bir müdahaleyi öne sürmesinin örnekleri de mevcuttur (örneğin genel görelilik kuramı). Bu işleyiş mantığı, “bilimin kendisi” ile tutarlı bir felsefi pozisyon arayanlara çok fazla seçenek bırakmamaktadır. Yazar için, iddia bir adım öteye taşınabilir: Galileo’dan günümüze görelilik fikrinin öyküsü, bilimin içsel mantığının zorunlu olarak diyalektik olduğunu ve herhangi bir başlıkta tutarlı bir felsefi pozisyonun ancak diyalektik materyalist bir bakış açısıyla mümkün olabileceğini örneklemektedir. Fizik biliminin içsel mantığının zorunlu olarak diyalektik olduğu ve (kavramı farklı bir içerikle kullanmakla birlikte) tarihsel bir evrime tabi olduğu yönündeki görüşler ilk kez burada dile getirilmiyor; I. Lakatos’un “Araştırma Programları Metodolojisi”, söz konusu görüşlerin başka bir örneğini oluşturmaktadır.[26] Tarihsellik anlayışı konusunda Lakatos'un yaklaşımını eleştirmekle birlikte, çalışmanın odağından uzaklaşmamak adına bu konuyu ele almayacağız.
Üzerine konuşulması gereken başka bir husus da, “nesnel bir maddi gerçeklik fikrinin görelilik ile birlikte zayıfladığı” iddiasını içeren yaklaşımlardır. Çalışmanın önceki bölümlerinde bu fikrin eleştirisi yer yer yapıldığı için, tekrar kapsamlı bir değerlendirmeye gerek olduğunu düşünmüyoruz. Bu fikre dayanan iddiaların temelinde çeşitli materyalist anlayışların geçersiz kabul edilmesi motivasyonunun yattığını öne sürmek mümkün olduğundan, eleştiriyi bu nokta üzerine yoğunlaştırabiliriz.
Hareketin göreliliği fikri Galileo’dan bu yana terk edilmemiş fikirlerden ve modern fiziğin temel taşlarından biridir. Dolayısıyla, öncelikle, materyalizmin terk edilmesi gerektiğini öne sürmek için Newton’cu hareket kuramının karşısına Einstein’cı hareket kuramını koymak saçmadır. Görelilik fikri, iki kuram arasındaki süreklilik ilişkisini temsil eden unsurlardan biridir.
İki kuram arasındaki süreklilik ilişkisini temsil eden başka bir unsur da, maddi gerçekliğin gözlemciden bağımsız bir karakterinin olduğu varsayımıdır. Esasında bu varsayım olmaksızın fizik yapmak mümkün değildir. Yine de, bu başlıkta bir kavram karmaşası yaşanması anlaşılabilir bir durumdur. Nesneleri tanımlamaya yarayan fiziksel özelliklerinin gözlemciden gözlemciye değişmemesi gerektiği düşüncesinde kendi başına bir sorun bulunmuyor. Örneğin bir nesnenin uzayda kapladığı bölge, o nesnenin sınırlarını çizmeye yarar ve dolayısıyla o nesne “gerçekse”, bu bölgenin tarifinin gözlemciden gözlemciye değişmemesi beklenebilir. Buradaki karışıklık, uzay ve zaman kavrayışımızın sıçramalı bir dönüşüm geçirdiğini gözden kaçırmakla ilgilidir. Bir nesneyi zamandan ve mekândan bağımsız, izole olarak tanımlayabileceğimiz varsayımı geçerliliğini yitirmiştir. Bu düşünce, maddenin temel yapıtaşları olarak ele aldığımız temel parçacıklara kadar ilerletilebilir; her ne kadar henüz bu noktaya gelmemiş olsak da.[27]
İki kuram arasındaki esas kopuş noktası, uzay-zamanın müdahale edilemez bir sahne olmaktan çıkıp, maddenin etkileyebildiği bir maddi varlığa dönüşmesidir. Bu noktanın, diyalektik materyalizm bağlamında hareket kuramlarını yorumlarken de en önemli nokta olduğunu öne sürmek mümkündür. Fizik bilimi, ilk kez olarak genel görelilik kuramı sayesinde, uzay-zamanı madde ve hareketin bir biçimi olarak kavrayabilmiştir. Genel göreliliğe ulaşılana kadar böyle bir düşüncenin hiç gündemde olmadığını söylemek abes olur; fizik literatüründe yaygınlaşmış olmasa da, örneğin Marksist klasiklerde konunun tartışıldığı bilinmektedir. Genel göreliliğin en önemli katkısı, diyalektik materyalist bakış açısıyla fizik bilimini icra etmeyi “teknik açıdan da mümkün” hale getirmiş olmasıdır. Galileo ve Newton için ancak hayal gücü sınırlarında olabilecek bir matematik bilgisi sayesinde bu mümkün olmuştur.
Uzay-zamanın maddi varlığın bir biçimi olarak görülmesi fikrinin başka bir kapıyı da kapattığı iddia edilebilir. Nesnel bir gerçeklik anlayışına sahip olan ancak maddi varlığı önceleyen bir “düşünsel” veya “ideal” nesnelliğin olduğu iddiasına yaslanan çeşitli yaklaşımlar da mevcuttur ve modern zamanlarda dahi bilim çevrelerinde ağırlık oluşturabilmektedir.[28] Bu konuyu, matematik felsefesinin etrafından dolaşarak ama hakkını da vererek tartışmak imkânsız olsa da, birkaç söz söylemek mümkündür.
Özel görelilik kuramı ile birlikte ulaşılan sonuçlardan biri, ünlü \(E=mc^2\) bağıntısıyla ifade edilen “kütle-enerji denkliği”dir. Bu bağıntı, kütleli bir nesnenin durgun göründüğü bir referans sisteminde bile sıfırdan farklı bir enerji içeriğine sahip olduğunu ifade eder. Dolayısıyla, kütle ve enerjinin, aynı fiziksel olgunun farklı biçimleri olduğunu ifade etmiş olur ki, bu çok güçlü bir argümandır.
Genel göreliliğin temel denklemi olan Einstein denklemi de, uzay-zaman geometrisini madde-enerji dağılımı cinsinden ifade eden bir eşitliktir. Bir anlamda, uzay-zaman ile madde arasında bir denklik ilişkisi kurar. Uzay-zamanı maddi varlığın bir biçimi olarak görme fikrinin teknik ifadesinin bu denklem olduğu söylenebilir.
Genel görelilik sayesinde, maddi varlıktan bağımsız bir uzay-zaman betimlemesi yapmak kavramsal olarak imkânsız hale gelmiştir.[29] Dolayısıyla, maddi varlığı önceleyen kurallardan, örneğin mutlak uzayın ve mutlak zamanın geometrisi gibi önsel kurallardan bahsetmek mümkün değildir. Dolayısıyla, maddi gerçekliği önceleyen başka bir gerçekliğin varsayıldığı yaklaşımların önemli ölçüde hasar aldığını iddia etmek mümkündür.[30]
Sonuç
Bu çalışmada, Galileo’dan günümüze kadar hareketin göreliliği fikrinin evrimi çeşitli örneklerle açıklanmaya çalışılmıştır. Bu evrimi doğru anlamanın görelilik kavramına dair çeşitli felsefi yanlışları ortadan kaldırmaya yarayacağı iddia edilmiş ve gösterilmeye çalışılmıştır. Çalışmanın sonunda, söz konusu evrimin bilimde tutarlı bir felsefi pozisyon tarifinin diyalektik materyalizm çerçevesinde mümkün olacağı savına ulaşılmıştır. Elbette ki bu sav, “tutarlılık arayışı”nın bilim insanının pratiğine etki eden bir nosyon olduğunu varsaymak durumundadır. Günümüzde bilim insanlarının büyük kısmı, bilime araçsalcı yaklaştığı veya farklı felsefi pozisyonlar benimsediği halde fizik biliminin sınırları içinde bilgi üretimine katılmaktadır. Bu çalışmanın iddiası ise, fizik biliminin bir “içsel mantığı” olduğu ve bunun tarih içinde, diyalektik yöntemle şekillendiğidir. Bu süreç, bilim insanlarının kolektif üretiminin sonucu olduğu için, bilim insanlarının tekil olarak tercih ettikleri felsefi konumlardan etkilense de, bu tekil konumların bir toplamı veya ortalaması olarak tarif edilemeyeceği için “içsel mantık” kavramına başvurulmaktadır. Bu çalışmada, hareketin göreliliği fikri üzerinden, söz konusu içsel mantığın nasıl işlediği gösterilmeye çalışılmıştır. Buradaki temel amaç, bu işleyişe dair çeşitli nedenlerle ortaya çıkan veya çıkabilecek karışıklıkların önlenmesi ve bu işleyişi doğru anlamayan çıkarımların eleştirilebilmesi için bir zemin sunmaktır.
Bununla birlikte, bu çalışmada diyalektik materyalizmin kategorileri bağlamında görelilik kavramı ve kuramlarının incelemesi yapılmamıştır. Ancak, bu bilinçli bir tercihtir. Bilimin her dalı, dolayısıyla fizik bilimi, bilim insanlarının kolektif üretimiyle gelişir ve şekillenir. Fizik camiası, her gün tekrar ettiği pratiğin tutarlı bir felsefi ilişki kurabildiği zeminin ne olduğu konusunda fikir birliğinde olmamasının yanında, böylesi bir konuyu tartışmanın gerekliliği konusunda bile fikir birliğinde değildir. Daha kötüsü, felsefi tartışmaların gereksiz olduğu düşüncesini benimseyen yaklaşımlar yaygındır ve yetişmekte olan kuşaklar büyük oranda bunların etkisi altındadır. Dolayısıyla, mevcut pratiğin, her gün tekrar ve tekrar icra edilen problem çözme / araştırma yapma / bilgi üretme eyleminin “bizim öznelliğimizden bağımsız olarak” nasıl bir işleyişe sahip olduğunun kavranması, felsefi tutarlılık arayışının bilim insanı için temel gereksinimlerden biri olduğunun görülmesini sağlayabilir. Görelilik fikrinin ve kuramlarının gelişim süreci (yaygın kabul uyarınca) modern bilimin miladından bugüne kadar süregelen ve bu arayışla ilgili hemen her unsurun örneğini barındıran bir süreç olduğu için, bu sürecin incelenmesinin felsefe problemleriyle fizik problemleri arasında yeniden ve geliştirici bir ilişkinin kurulabilmesi açısından öğretici olacaktır. Okuduğunuz metinde, böylesi bir incelemenin içereceği bazı başlıkları sunmayı amaçladım; metnin sunamadığı başlıklar için teşvik edici olması ise, kuşkusuz, en büyük beklentimdir.
Kaynaklar:
Bernal, J. D. (2008). Tarihte Bilim. (T. Ok, Çev.). İstanbul: Evrensel Basım Yayın.
Britannica. (2020). Michelson-Morley experiment. Erişim tarihi 30 Nisan 2020. https://www.britannica.com/science/Michelson-Morley-experiment#/media/1/380069/17906
Cheng, D. (1993). Fundamentals of Engineering Electromagnetics. ABD: Addison-Wesley Publishing Company, Inc.
Einstein, A. (1990). On the electrodynamics of moving bodies. Stachel, J., Cassidy, D. C., Renn, J. ve Schulmann, R. (Ed.), The Collected Papers of Albert Einstein, Volume 2: The Swiss Years: Writings, 1900-1909 (ss. 275-310) ABD: Princeton University Press.
Giancoli, D. (2008). Physics for Scientists and Engineers for Modern Physics. 4. Baskı. New Jersey, ABD: Pearson Prentice Hall.
Goldstein, H., Poole, C., Safko, J. (2000). Classical Mechanics. 3. Bakı. Addison Wesley.
Jackson, J. D. (2001). Classical Electrodynamics. 3. Baskı. ABD: John Wiley & Sons, Inc.
Lakatos, I. (2017). Yanlışlama ve bilimsel araştırma programlarının metodolojisi. Lakatos, I. ve Musgrave, A. (Ed.), Eleştiri ve bilginin gelişmesi (ss. 123-246), (N. Küçük, Çev.) İstanbul: İthaki Yayınları.
Misner, C., Thorne, K., Wheeler, J. A. (1973). Gravitation. San Francisco, ABD: W. H. Freeman and Company.
Olpak, M. A. (2019). “Eleştirel bir Lakatos okumasına nereden başlamalı?”. Madde, Diyalektik ve Toplum, 3 (2), 198-206.
Rindler, W. (2006). Relativity: Special, General and Cosmological. 2. Baskı. ABD: Oxford University Press.
Stanford Encyclopedia of Philosophy (2017). Galileo Galilei. https://plato.stanford.edu/entries/galileo/#3 Erişim tarihi: 13.05.2020
van Dongen, J. (2009). On the Role of the Michelson–Morley Experiment: Einstein in Chicago. Arch. Hist. Exact Sci
[1] Çembersel yörüngeler dinsel kutsiyete uygun görülen şekillerdi. Bu husus ilk olarak Kepler tarafından eliptik yörünge hipotezi vasıtasıyla düzeltilmiştir (Bernal, 2008: 370).
[2] Bu konu metnin ilerleyen kısımlarında açıklanmaktadır.
[3] Burada başka bir önemli husus daha vardır: Bir cismin, kendisine bir kuvvet uygulanmaksızın hareket halinde olabileceği fikri, Aristo’nun doktrinine aykırıdır. Aristo’ya göre hareket ancak ve ancak bir kuvvetin varlığında mümkün olan bir olgudur. Galileo’ya göre ise, üzerine hiçbir kuvvet etki etmeyen bir cisim, başka bir cisme hareketli görünebilir. Bu durum sadece cisimlerin birbirine göre hareket halinde oldukları anlamına gelecektir.
[4] Gündelik yaşamdan da bilinen bir örnek “Coriolis etkisi”dir; bkz. Goldstein vd., 2000:174-180.
[5] Görelilik ilkesi elbette ki Newton’un hareket yasaları ile sınırlı değildir. “Fiziğin yasalarının tüm eylemsiz gözlemcilere göre aynı olması gerekir”. Bu çalışmada, anlatımın sadeliğini korumak adına, konuyu cisimlerin hareket ilişkileri üzerinden açıklamaya çalışacağız.
[6] Anlatımı karmaşık hale getirmemek adına, burada bahsi geçen fiziksel niceliklerin birimlerinden söz edilmemiştir. Hesaplamalarda, fiziksel niceliklerin birimlerinin olduğunun unutulmaması gerekir. Örneğin, gözlemcilerimizin zamanı saniye cinsinden, konumu da metre cinsinden ölçtüğünü düşünebiliriz.
Dikkat edilmesi gereken başka bir nokta, konum değişkeninin mesafe anlamına gelmemesidir. Konum, mesafe ile ilişkilidir. Uzaydaki her noktaya, belirli bir referans noktasına atıfla (en genelde) üç adet koordinat değeri atayabiliriz. Bu üç koordinatın bileşiminden oluşan nicelik, cismin konum vektörüdür. İki nokta arasındaki mesafe ise Pisagor teoremi ile hesaplanır: mesafenin karesi, noktaların koordinat farklarının kareleri toplamına eşittir. Konum değişkeni bir vektörken (yönlü nicelik), mesafe skaler (yönsüz) bir niceliktir.
[7] Bu notasyon Newton’un kullandığı notasyondur. Konvansiyonel türev notasyonları arasında görece basit bir versiyon olduğu için halen yaygın olarak kullanılmaktadır.
[8] Fizik kitaplarında bu açıklama “Kişinin öne doğru bir kuvvet varmış gibi hissetmesinin nedeni kişinin eylemsizliğidir.” denir. Kast edilen, eylemsizlik niceliğidir. Burada kişi eylemsiz gözlemci değildir, ancak, sahip olduğu kütle ve bunun uzaya dağılımı ile ölçülen bir “eylemsizlik niceliğine“ sahiptir: Eylemsizlik kütlesi (inertial mass) ve eylemsizlik momenti (moment of inertia) (yukarıdaki örnekte sadece eylemsizlik kütlesinin etkisi görülmektedir).
[9] En hassas kavramla, ivme vektörü.
[10] Açık ki, kast edilen, “durgunluk”, “hareketin yokluğu” anlamında değişmezlik değildir. Dilimizin kavram dağarcığını geliştirmemiz gerekmektedir.
[11] Bu argümanı ispatlamak zor değildir, ancak tartışmamız açısından gerekli olmadığı için okurun tercihine bırakabiliriz.
[12] Bu kavram daha ziyade yüksek enerji fiziği literatüründe kullanılsa da bir kavram olarak fizik biliminin her alanında kullanılmasının önünde bir engel bulunmamaktadır.
[13] Bilim insanlarının, felsefeye hiç başvurmaksızın çalışmaya başladığı ima edilmemektedir. Buradaki vurgu, tekil olarak bilim insanlarının değil, bilim camiasının kolektif eyleminin bir sonucu olarak kuramların gelişmesi, yenilerinin ortaya çıkması ve benzeri süreçlerde felsefi tartışmalar yerine teknik becerileri geliştirme potansiyelinin belirleyici hale gelmiş olmasına yapılmaktadır. Elbette, hangi kuramın teknik becerilerimizi geliştirmek açısından daha değerli olduğu sorusu halen felsefi bir sorudur; ancak önemli olan, bu sorunun başat soru haline gelmiş olmasıdır.
[14] Kuramın içerisinde “burjuvazi” sözcüğünün geçmemesi önemli değildir; her kuram, onu icra eden insanlar tarafından tarih içinde geliştirilir. Bir kuramı çalışarak bilgi üreten ve yayan insanlar yoksa, kuramın herhangi bir bilim tarihi yazınında herhangi bir epistemoloji kuramı uyarınca değerlendirilmesinin bir anlamı olmayacaktır.
[15] Nazire yaparak: Die Logik der Wissensproduktion (çeviri önerisi için Ceren Tuğlu Olpak’a teşekkür ediyorum).
[16] Birleşik kuram kavramının ilk örneği olarak Maxwell’in formülasyonuyla elektromanyetizma kuramı gösterilebilir. Bir birleşik kuram, birbirinden farklı görünen ancak aynı temel olgunun farklı yansımaları olarak ifade edilebilen olguların tamamını, bahsi geçen temel olgu cinsinden izah eden bir kuramdır.
[17] Manyetik alanın tek düze olması demek, bulunduğu bölgede her noktada aynı büyüklükte ve aynı yöne bakan bir manyetik alan vektörünün tanımlanmış olması demektir.
[18] Rijit: Hareket esnasında biçim değişikliğine uğramayan.
[19] Ayrıntılar için, bkz. Jackson, 2001: 516, 558.
[20] Einstein, özel görelilik kuramının temeli olan “Yüklü cisimlerin elektrodinamiği üzerine” (Einstein, 1990) başlıklı makalesini yazarken deneyin içeriğine ve sonuçlarına vakıf değildir. Bu argüman, kendi ifadeleri ve çeşitli bilim tarihi tartışmaları ile oluşmuş ve güncel literatürde yer alan ortak görüşün ifadesi olarak ele alınabilir; bkz. v. Dongen, 2009.
[21] Ayrıntılar için bkz. (Giancoli, 2008: 960)
[22] Esasen burada koordinat dönüşümlerini ele almak gerekir. Einstein’cı görelilik ilkesine uyan koordinat dönüşümleri (Lorentz dönüşümleri), gözlemicilerin birbirine göre hızı ışık hızından çok küçük olduğu zaman Galileo’cu görelilik ilkesine uyan koordinat dönüşümlerine indirgenir (Rindler, 2006: 47).
[23] Temel matematikte öğrendiğimiz limit alma işlemi kast edilmektedir.
[24] Kuşkusuz, N. Bohr bu iddiaya kuşkuyla bakardı. Ancak iddianın temeli şudur: Bir sistemden enformasyon almak için o sistem üzerinde ölçüm yapmanız gerekir. Ölçüm işlemi fiziksel etkileşim olmaksızın gerçekleşemez ve ölçen ile ölçülen arasındaki her etkileşim, ölçülenin fiziksel durumunu (en azından potansiyel olarak) etkiler. Bu etki üzerindeki kontrolümüz ise yine fiziksel nedenlerle sınırlıdır. Sınırı ifade eden bağıntı, kesinsizlik bağıntısıdır (uncertainty relation).
[25] Kaynağın yayın tarihi itibarıyla.
[26] Lakatos’un yaklaşımına dair eleştiriler için şu çalışmalar incelenebilir: Olpak, 2019.
[27] Amacımız spekülasyon yapmak değildir. Söz konusu argüman, Einstein’cı yeni fiziğin ne denli güçlü iddiaları olabileceğini göstermek açısından değerlidir.
[28] Bizzat Lakatos'un kendisi ve K. Popper en popüler örnekler arasındadır, bkz. (Lakatos, 2017: 224).
[29] Fizikçilerden “vakum çözümlerini nasıl yorumlayacağız” sorusu gelecektir. Buradaki sorun, fizik jargonunda uzay-zaman ile madde kavramları arasına halen bir sınır çekiliyor olmasıdır. Teknik açıdan anlaşılır bir durum olsa da, genel görelilik bu sınırı kavramsal olarak ortadan kaldırmıştır. Kast edilen budur.
[30] Fiziğin yasalarının olması, halen böyle bir iddiayı desteklemez mi? Yasalar, ilkeler, kuramlar arasındaki diyalektik ilişkinin, bu kategorileri maddi gerçekliği önceleyen kategoriler olarak tanımlamamızı imkânsız kıldığı ifade edilmelidir. Yasalar varsa, yasa değişiklikleri de olmaktadır.