Bir dakikada matematik: Voronoi şemaları

Acilen hastaneye gitmeniz gerekiyor ve haritaya bakıyorsunuz. Birinin diğerinden daha yakın olduğuna nasıl karar verirsiniz?

[BAA - Matematik / Çeviri: Oğuz Şavk]

Çok sayıda hastanesi olan bir şehir düşünün. Birisinin acil durumu olduğunda, her zaman bulundukları yere en yakın hastaneye gitmesini veya götürülmesini istersiniz. İhtiyacınız olan şey, her hastanenin havzasını gösteren bir harita: o bölgedeki herkes için, hangi hastanenin diğerlerinden daha yakın olduğu gösteren. Bunu nasıl yaparsınız?

Zor değil, sadece elle yaparsanız muhtemelen biraz sıkıcı. Haritadaki A ve B noktalarında bulunan iki hastane ile başlayın. Onları birbirine bağlayan doğru parçasını çizin, o doğru parçasının orta noktasını bulun ve daha sonra bu orta noktadan geçen ve A'dan B'ye olan parçaya dik olan çizgiyi çizin. Bu çizgi şehri iki bölgeye ayırıyor. Bunlardan biri, A'yı içeren, A'ya B'den daha yakın olan tüm noktaları içerir. Diğeri, B'ye A'dan daha yakın olan tüm noktaları içerir. Çizgideki noktalar A ve B ile aynı mesafedir.

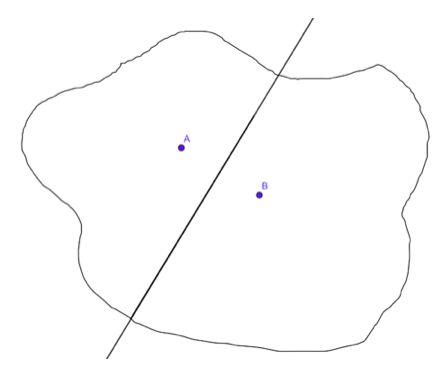
Şimdi üçüncü hastaneye, C noktasına bakın. Yukarıda yaptığımız şeyi tekrarlayarak, A'ya C'den daha yakın olan noktaların bölgesini ve B'ye C'den daha yakın olan noktaların bölgesini hesaplarsınız.

Tüm hastaneleri hesaba katana kadar kesişen bölgeleri bulmaya devam edersiniz. Sonunda ulaştığınız resme, haritanın verilen noktalardan birine diğerinden daha yakın olan noktaların bölgelerine bölünmesine, Voronoi şemaları denir. İsmini Rus matematikçi Gregory Voronoi'den (1868-1908) almıştır.

Tahmin edebileceğiniz gibi Voronoi şemaları türlü türlü alanda faydalıdır. Örneğin, ormanların büyüme modellerini incelemek için kullanılabilir veya robotların bir dizi engelden net yollar bulmasına yardımcı olabilirler.

Ama bir sebepten dolayı tıbbi benzetmeyi seçtik. 1850'lerde, kolera salgını Londra'da Soho'yu yok ediyor, nüfusun %10'unu öldürüyor ve günler içinde tüm aileleri yok ediyordu. Hastalığın "kötü hava" dan kaynaklandığı düşünülüyordu, ancak doktor John Snow'un başka bir fikri vardı: koleranın, o günlerde şehir boyunca konumlandırılmış pompalardan gelen kirli su kaynaklarından geldiğini düşünüyordu.

İlk önce bir Soho haritasında her adresteki ölüm sayısını işaretleyerek diğerlerine teorisini inandırabildi. Daha sonra 40 Broad Caddesi'ndeki (şu anda Broadwick Caddesi) belirli bir su pompasının "havzasını" belirledi. Bu havzadaki noktalar Broad Street pompasına diğer tüm pompalardan daha yakındı. Sadece yukarıdaki örneğimizden farklı olarak, Snow bir karganın uçacağı doğrudan mesafeyi değil, sokaklar ve sokaklar arasındaki yürüme mesafesini kullandı. Haritada işaretlenen neredeyse tüm ölümlerin Broad Street pompasının havzası içinde olduğu ortaya çıktı ve anekdotsal kanıtları, anlaşılamayan birkaç vakayı açıkladı.

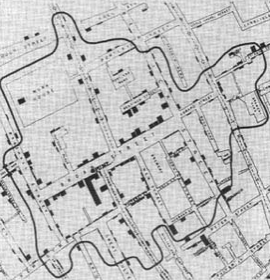
Bu, kirlenmiş suyun gerçekten koleranın nedeni olduğunu çok inandırıcı bir şekilde gösterdi. Bugün pompanın bir zamanlar durduğu yer bir anıtla işaretlenmiş ve hemen yanında John Snow'un onuruna adlandırılan bir bar var.

Kaynak:

Plus Magazine, Maths in a minute: Voronoi diagrams, https://plus.maths.org/content/maths-minute-voronoi-diagrams