Bir dakikada Matematik: Euler Formülü

İşte matematiksel formüller arasındaki güzellik kraliçesine hızlı bir giriş.

[BAA – Matematik/ Çeviri Haber: Büşra Atar]

Euler formülü sıklıkla matematikteki en güzel formül olarak tanınır. İnsanlar formül baskılı tişörtlerini giyerler ve vücutlarına dövmesini yaptırırlar. Neden?

Bu formül

\( e^{i \pi} +1 = 0, \)  

diye okunur ve buradaki \( e= 2.7182818284...\) doğal logaritmanın tabanıdır \( \pi = 3.1415926535...\), bir dairenin çevresi ile çapı arasındaki orandır ve \(i =\sqrt{-1}\). Bu üç sabit sayı matematikte son derece önemlidir- ve eşitlik aynı zamanda 0 ve 1'i içerdiğinden, matematikteki en önemli sayıların beşini en önemli matematiksel işlemlerden ve ilişkilerden dördünü birleştiren bir formüle sahibiz - toplama, çarpma, üs alma ve eşitlik. Bu yüzden matematikçiler Euler formülünü çok seviyorlar.

Peki bu formül nereden geliyor ve anlamı ne? Yukarıda bahsettiğimiz gibi \(i =\sqrt{-1}\) Negatif sayıların kare kökleri olmadığı farz edildiği için bu şok edici görünebilir. Ancak, basit bir şekilde \( -1 \) 'in bir karekökü olduğuna hüküm getirirsek ve \( i \) olarak adlandırırsak, karmaşık sayılar adı verilen yeni bir sayı sınıfı inşa edebiliriz. Karmaşık sayılar \( x+iy \) biçimindedir; burada \( x \) ve \( y \) sıradan gerçel sayılardır ( \( x=0 \) ve \( y=1 \) gerçek sayıları için \( i \) karmaşık sayısı bulunur). Gerçel bir sayının karmaşık bir sayı olarak da görülebileceğini unutmamak gerekir. Örneğin \( -1 \), \( x= -1 \)  ve \( y=0 \) için karmaşık bir sayıdır.

Tıpkı gerçel bir sayının sayı çizgisindeki bir nokta ile temsil edilmesi gibi, \( z \) karmaşık sayısı da düzlemdeki bir nokta ile temsil edilir. \( z = x+iy \) karmaşık sayısını \( (x,y) \) koordinatlarıyla ifade edilen nokta ile ilişkilendiririz.

Bu tasvirde kartezyen koordinatları kullandık, bu bir noktanın konumunu, yatay yönde ne kadar yürüyeceğinizi ve dikey yönde ne kadar yürüyeceğinizi söyleyerek tanımlar. Bununla birlikte, bir noktanın konumunu aşağıda gösterildiği gibi iki eksenin kesişme noktasından başlayan ok ile tarif etmek bazen daha uygundur.

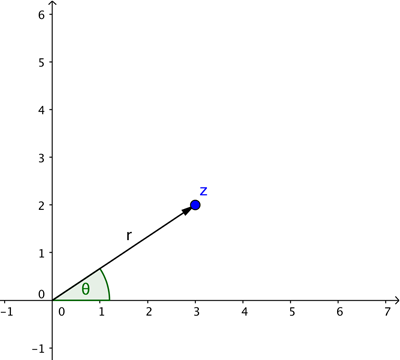
Bu oku tanımlamak için uzunluğu \( r \) ve pozitif \( x \)-ekseni ile (saat yönünün tersine) yaptığı \( \theta \) açısına ihtiyacınız vardır. Bunlar bizim noktamızın kutupsal koordinatlarıdır. Temel trigonometri bize şunu söyler; eğer bir nokta \( (x,y) \) kartezyen koordinatlarına ve \( (r, \theta) \) kutupsal koordinatlarına sahipse o zaman aşağıdaki şemada gösterildiği gibi, \( x=r \cos {(\theta )} \) ve \( y=r \sin {(\theta )}. \)

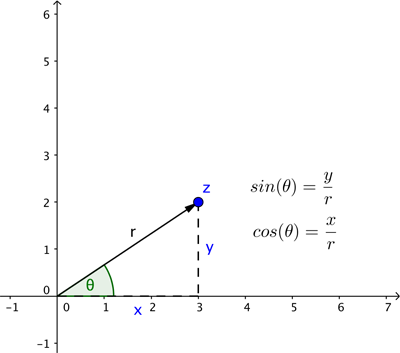
Bu nedenle, noktamızın temsil ettiği \( z \) karmaşık sayısı olan \( x+iy \), şu şekilde de yazılabilir:

\( z= r (\cos {(\theta )}+i\sin {(\theta )}). \)

İşte can alıcı nokta geliyor. Tesadüfe bakın ki, \( r \) ve \( \theta \) gerçek sayıları için

\(  r(\cos {(\theta )} + i \sin {(\theta )}) = re^{i\theta }. \)

Bunu kuvvet serilerini kullanarak kanıtlayabilirsiniz. Üstel fonksiyon ile sinüs ve kosinüs olmak üzere iki trigonometrik fonksiyonun bu şekilde bağlanması güzel bir olgudur. Ve bu herhangi bir \( z \) karmaşık sayısının \( re^{i \theta}\) olarak yazılabileceği anlamına gelir; burada \( r \), düzlemdeki \( z \) ile ilişkili noktayı eksenlerin kesişim noktasına bağlayan çizginin uzunluğudur ve \( \theta \) bu çizginin pozitif  \( x \)-ekseni ile (saat yönünün tersine) yaptığı açıdır.

Bu artık Euler eşitliğini açıklığa kavuşturuyor \( e^{i\pi } = 1 \times e^{i \pi} \) karmaşık sayısı, düzlemde \( \pi \) açısı ile ilişkili ve eksenlerin kesişim noktasından \( 1 \) mesafesindeki noktayı temsil eder. İşte bu nokta, \( -1 \) karmaşık sayısını temsil eden \( (-1,0) \) kartezyen koordinatlarına sahip noktadır.

Bunların hepsini bir araya toplarsak

\( e^{i\pi } = -1, \)

olduğunu görürüz. Bu demek oluyor ki

\( e^{i\pi }+1 = 0. \)

Ve adı geçen Euler formülü.

Kaynak:

Plus Magazine, Maths in a Minute: Euler’s identity, https://plus.maths.org/content/maths-minute-eulers-identity